如图，在矩形ABCD中，AB＝8，BC＝6，点O为对角线BD的中点，点P从点A出发，沿折线AD－DO以每秒1个单位长度的速度向终点O运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．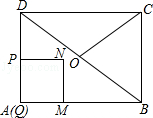
（1）求点N落在BD上时t的值；
（2）直接写出点O在正方形PQMN内部时t的取值范围；
（3）当点P在折线AD－DO上运动时，
①求S与t之间的函数关系式；
②直接写出DN平分△BCD面积时t的值．
北京时间2010年4月14日7时49分，青海玉树发生7.1级地震，灾情牵动着全国各族人民的心。某中心校组织了捐款活动．小华对八年级（1）（2）班捐款的情况进行了统计，得到如下三条信息：
信息一：（1）班共捐款540元，（2）班共捐款480元．
信息二：（2）班平均每人捐款钱数是（1）班平均每人捐款钱数的
．
信息三：（1）班比(2)班少3人．
请你根据以上三条信息，求出八（1）班平均每人捐款多少元？
如图，在四边形ABCD中，∠B =90°，AB=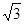
，∠BAC =30°，CD=3，AD=
，求∠ACD的度数。
如图，已知平行四边形ABCD中，点
为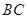
边的中点，连结DE并延长DE交AB延长线于F. 求证：
．
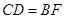计算：
A、B两地相距36千米.甲从A地出发步行到B地，乙从B地出发步行到A地.两人同时出发，4小时后相遇；6小时后，甲所余路程为乙所余路程的2倍.求两人的速度.