如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y 轴于点N,再分别以点M、N为圆心,大于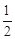 MN的长为半径画弧,两弧在第二象限交 于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为()
MN的长为半径画弧,两弧在第二象限交 于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为()
| A.a=b | B.2a+b=﹣1 | C.2a﹣b=1 | D.2a+b=1 |
已知两个变量 和
和 ,它们之间的3组对应值如下表所示, 则y 与x之间的函数关系式可能是( )
,它们之间的3组对应值如下表所示, 则y 与x之间的函数关系式可能是( )
| x |
-1 |
0 |
1 |
| y |
-3 |
-4 |
-3 |
A. B.
B. C.
C. D.
D.
如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D,B,使得A,D,B在一条直线上,且与河的边沿垂直,测得BD=10m,然后又在垂直AB的直线上取点C,并量得BC=30m.如果DE=20m,则河宽AD为()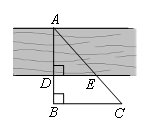
| A.20m | B.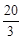 m m |
C.10 m | D.30 m |
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为()
A.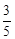 |
B.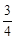 |
C.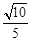 |
D.1 |
如图,A,B,C是⊙O上的三个点,若∠C=35°,则∠AOB的度数为()
| A.35° | B.55° | C.65° | D.70° |