粒子回旋加速器的工作原理如图所示,置于真空中的D型金属盒的半径为R,两金属盒间的狭缝很小,磁感应强度为B的匀强磁场与金属盒盒面垂直,高频率交流电的频率为f,加速器的电压为U,若中心粒子源处产生的质子质量为m,电荷量为+e,在加速器中被加速。不考虑相对论效应,则下列说法正确是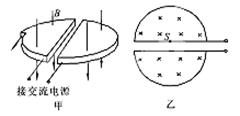
| A.质子被加速后的最大速度不能超过2πRf |
| B.加速的质子获得的最大动能随加速电场U增大而增大 |
C.质子第二次和第一次经过D型盒间狭缝后轨道半径之比为 |
| D.不改变磁感应强度B和交流电的频率f,该加速器也可加速a粒子 |
如图为一空间探测器的示意图,P1、P2、P3、P4四个喷气发动机,P1、P3的连钱与空间一固定坐标系的x轴平行,P2、P4的连线与y轴平行,每台发动机开动时,都能向探测器提供推力,但不会使探测器转动.开始时,探测器以恒定的速率v0向正x方向平动.要使探测器改为向正x偏负y 60º的方向以原来的速率v0平动,则可()
| A.先开动P1适当时间,再开动P4适当时间 |
| B.先开动P3适当时间,再开动P2适当时间 |
| C.开动P4适当时间 |
| D.先开动P3适当时间,再开动P4适当时间 |
如图所示,一个劈形物体M各面均光滑,上面成水平,水平面上放一光滑小球m,现使劈形物体从静止开始释放,则小球在碰到斜面前的运动轨迹是(斜面足够长)()
| A.沿斜面向下的直线 | B.竖直向下的直线 |
| C.无规则曲线 | D.抛物线 |
在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体 , 与竖直墙之间放一光滑圆球 ,整个装置处于静止状态。现对 加一竖直向下的力 , 的作用线通过球心,设墙对 的作用力为 , 对 的作用力为 ,地面对 的作用力为 。若 缓慢增大而整个装置仍保持静止,截面如图所示,在此过程中()

| A. | 保持不变, 缓慢增大 |
| B. | 缓慢增大, 保持不变 |
| C. | 缓慢增大, 缓慢增大 |
| D. | 缓慢增大, 保持不变 |
用轻弹簧竖直悬挂质量为 的物体,静止时弹簧伸长量为 。现用该弹簧沿斜面方向拉住质里为 的物体,系统静止时弹簧伸长量也为 。斜面倾角为 ,如图所示。则物体所受摩擦力()

| A. | 等干零 |
| B. | 大小为 ,方向沿斜面向下 |
| C. | 大小为 ,方向沿斜面向上 |
| D. | 大小为 ,方向沿斜面向上 |
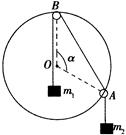 如图所示,小圆环A吊着一个质量为m2的物块并套在另一个竖直放置的大圆环上,有一细线一端拴在小圆环A上,另一端跨过固定在大圆环最高点B的一个小滑轮后吊着一个质量为m1的物块。如果小圆环、滑轮、绳子的大小和质量以及相互之间的摩擦都可以忽略不计,绳子又不可伸长,若平衡时弦AB所对应的圆心角为α,则两物块的质量比m1∶m2应为
如图所示,小圆环A吊着一个质量为m2的物块并套在另一个竖直放置的大圆环上,有一细线一端拴在小圆环A上,另一端跨过固定在大圆环最高点B的一个小滑轮后吊着一个质量为m1的物块。如果小圆环、滑轮、绳子的大小和质量以及相互之间的摩擦都可以忽略不计,绳子又不可伸长,若平衡时弦AB所对应的圆心角为α,则两物块的质量比m1∶m2应为
A.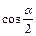 |
B.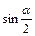 |
C.2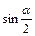 |
D.2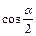 |