（本小题满分9分）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．
（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；
（2）如图2，连接AA1，CC1．若△ABA1的面积为4，求△CBC1的面积；
（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．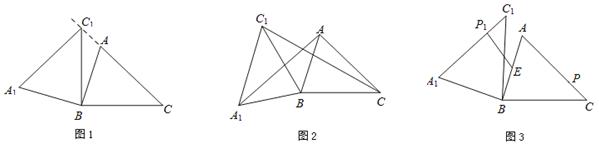
解方程（组）：
（1）
；
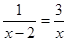（2）
化简：
（1）
；
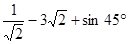（2）
如图，形如量角器的半圆O的直径DE=12cm，形如三角板的△ABC中，∠ACB=90°，∠ABC=
30°，BC=12cm．半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t (s)，当t=0s时，半圆O在△ABC的左侧，OC=8cm．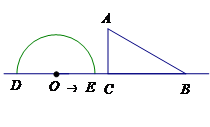
（1）当t为何值时，△ABC的一边所在的直线与半圆O所在的圆相切？
（2）当△ABC的一边所在的直线与半圆O所在的圆相切时，如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积．
在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子，镜子的长与宽的比是2：1，已知镜面玻璃的价格是每平方米120元，边框的价格是每米30元，另外制作这面镜子还需加工费45元．设制作这面镜子的总费用是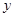
元，镜子的宽是
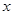米．
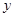（1）求与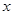之间的关系式．
（2）如果制作这面镜子共花了195元，求这面镜子的长和宽．
在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90°．
（1）判断下列命题的真假（在相应括号内填上“真”或“假”）：
①等腰梯形是旋转对称图形，它有一个旋转角为180°．（）
② 矩形是旋转对称图形，它有一个旋转角为180°．（）
（2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是．（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形 ．
（3）写出两个多边形，它们都是旋转对称图形，都有一个旋转角为72°，并且分别满足下列条件：
①是轴对称图形，但不是中心对称图形；②既是轴对称图形，又是中心对称图形．