如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
(年湖南衡阳10分)二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0)、B(1,0)两点,与y轴交于点C(0,﹣3m)(其中m>0),顶点为D.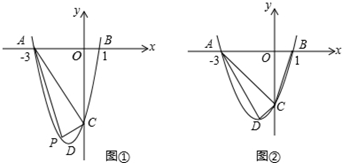
(1)求该二次函数的解析式(系数用含m的代数式表示);
(2)如图①,当m=2时,点P为第三象限内的抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;
(3)如图②,当m取何值时,以A、D、C为顶点的三角形与△BOC相似?
(年湖南常德10分)如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.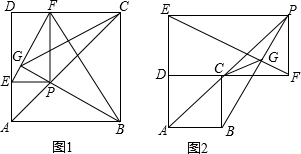
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.
(2014年黑龙江哈尔滨3分)如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .
的值为 .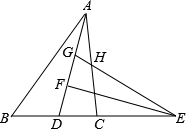
(年广西贵港10分)如图,AB是大半圆O的直径,AO是小半圆M的直径,点P是大半圆O上一点,PA与小半圆M交于点C,过点C作CD⊥OP于点D.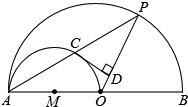
(1)求证:CD是小半圆M的切线;
(2)若AB=8,点P在大半圆O上运动(点P不与A,B两点重合),设PD=x,CD2=y.
①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当y=3时,求P,M两点之间的距离.
(年广东梅州10分)如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△FED是直角三角形时,求x的值.