如图所示，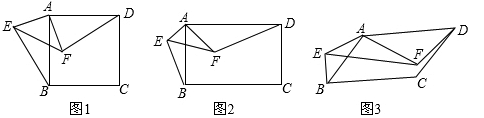
（1）正方形ABCD及等腰Rt△AEF有公共顶点A，∠EAF=90°，连接BE、DF．将Rt△AEF绕点A旋转，在旋转过程中，BE、DF具有怎样的数量关系和位置关系？结合图（1）给予证明；
（2）将（1）中的正方形ABCD变为矩形ABCD，等腰Rt△AEF变为Rt△AEF，且AD=kAB，AF=kAE，其他条件不变．（1）中的结论是否发生变化？结合图（2）说明理由；
（3）将（2）中的矩形ABCD变为平行四边形ABCD，将Rt△AEF变为△AEF，且∠BAD=∠EAF=a，其他条件不变．（2）中的结论是否发生变化？结合图（3），如果不变，直接写出结论；如果变化，直接用k表示出线段BE、DF的数量关系，用a表示出直线BE、DF形成的锐角β．
正方形ABCD中，点E、F为对角线BD上两点，DE=BF
（1）四边形AECF是什么四边形？ 为什么？
（2）若EF=4cm，DE=BF=2cm，求四边形AECF的周长。
如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式；
（2）根据图像回答：当x取何值时
（3）根据图像回答：当x取何值时
已知：如图，在
ABCD中，E、F是对角线AC上的两点，且AE＝CF，求证：DE＝BF
已知一次函数y＝kx＋b的图象经过点（－1，－4），且与正比例函数y＝x+1的图象相交于点（2，a），求
（1）a的值
（2）k，b的值
（3）这两个函数图象与x轴所围成的三角形面积.
某商场用36000元购进A、B两种商品，销售完后共获利6000元，其进价和售价如下表：
| A |
B |
|
| 进价（元/件） |
120 |
100 |
| 售价（元/件） |
138 |
120 |
（1）该商场购进A、B两种商品各多少件；（注：获利
售价
进价）
（2）商场第二次以原进价购进A、B两种商品．购进
种商品的件数不变，而购进
种商品的件数是第一次的2倍，种商品按原售价出售，而种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于8160元，B种商品最低售价为每件多少元