四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.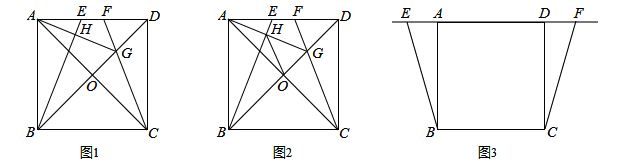
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
(本题8分)在平面直角坐标系xOy中,已知点P(3,4),点Q在x轴上,△PQO是等腰三角形,在图中标出满足条件的点Q位置,并写出其坐标.
(本题7分)某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设每户家庭用水量为x立方米时,应交水费y元.
(1)当0≤x≤20时,y与x的函数关系式为 ;
当x>20时,y与x的函数关系式为 。
(2)小明家第二季度交纳水费的情况如下:
| 月份 |
四月份 |
五月份 |
六月份 |
| 交费金额 |
30元 |
34元 |
47.8元 |
小明家这个季度共用水多少立方米?
(本题8分)如图,已知菱形ABCD的对角线相交于O,延长AB至E,使BE=AB,连结CE.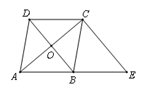
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
(本题6分)如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
(本题6分) 如图,Rt△ABC中,∠C=90°,AC=BC,AB=4,试建立适当的直角坐标系,写出各顶点的坐标.