电动蛙式打夯机(图甲)是利用冲击和冲击振动来夯实、平整场地的机械,由电动机、皮带轮、偏心块、夯架、夯锤等组成(图乙)。启动电动机,在旋转着的偏心块离心力作用下,夯架绕后轴上下摆动,当夯架向下摆动时夯锤就夯击土层,向上摆动时使打夯机前移,故每夯击一次,机身即向前移动一次。右表是某型号电动蛙式打夯机的部分参数(设夯锤夯击土层的能量全部用于夯实土层)。

(1)若打夯机以10m/min 的平均速度沿直线前进,则10min 前进了多少米?
(2)为了估算某次夯锤夯击土层时的冲击力,小明将重为4N、底面积为1cm2的圆柱体竖直平放在被夯击土层上,土层被压下的深度与夯锤夯击的深度相同,则此次夯击时的平均冲击力为多少牛?
(3)施工时,若打夯机前移消耗的能量为200J/次,则打夯机的机械效率是多少?
如图所示,一半径为R=0.2m的竖直粗糙圆弧轨道与水平地面相接于B点,C.D两点分别位于轨道的最低点和最高点.距地面高度为h=0.45m的水平台面上有一质量为m=1kg可看作质点的物块,物块在水平向右的恒力F=4N的作用下,由静止开始运动,经过t=2s时间到达平台边缘上的A点,此时撤去恒力F,物块在空中运动至B点时,恰好沿圆弧轨道切线方向滑入轨道,物块运动到圆弧轨道最高点D时对轨道恰好无作用力.物块与平台间的动摩擦因数μ=0.2,空气阻力不计,取 g=10m/s2.求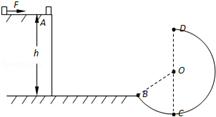
(1)物块到达A点时的速度大小vA.
(2)物块到达B点时的速度大小vB.
(3)物块从B点运动到D点过程中克服摩擦力所做的功.
(8分) 航模兴趣小组设计出一架遥控飞行器,其质量m=2㎏,动力系统提供的恒定升力F=28N,飞行器飞行时所受的阻力大小f=4N且保持不变,g取10m/s2.试飞时,飞行器从地面由静止开始竖直上升,12s后飞行器因故立即失去升力无法修复.求:
(1)正常飞行t1=12s到达高度h1;
(2)飞行器还能上升的高度h2;
在足够长的水平光滑直导轨上,静止放着三个质量均为m=1 kg的相同小球A.B.C,现让A球以v0=2 m/s的速度正对着B球运动,A.B两球碰撞后粘在一起,两球继续向右运动并与C球发生正碰,C球的最终速度vC=1 m/s。求:
①A.B两球与C球相碰前的共同速度多大?
②两次碰撞过程中一共损失了多少动能?
一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m处下潜到深度为h2时,看到标记刚好被浮标挡住,此处看不到船尾端Q;继续下潜△h=2.0m,恰好能看见Q.(已知水的折射率n= )求
)求
①深度h2;
②赛艇的长度l.(可用根式表示)
如图所示,A气缸截面积为500 cm2,A.B两个气缸中装有体积均为10 L、压强均为1 atm、温度均为27 ℃的理想气体,中间用细管连接.细管中有一绝热活塞M,细管容积不计.现给左面的活塞N施加一个推力,使其缓慢向右移动,同时给B中气体加热,使此过程中A气缸中的气体温度保持不变,活塞M保持在原位置不动.不计活塞与器壁间的摩擦,周围大气压强为1 atm=105 Pa,当推力F=×103 N时,求:
①活塞N向右移动的距离是多少?
②B气缸中的气体升温到多少?