自动饮水机已经普遍用于车站、学校等公共场所,它的简化电路图如图所示, 电热丝电阻分别为R1、R2,请根据说明书提供的信息计算(水的密度ρ水=1×103 kg/m3,水的比热容C水=4.2×103 J/kg℃)
| 饮水机参数 |
| 热水温度:≥90 ℃ |
| 热胆容积:2 L |
| 额定功率:1000 W |
| 保温功率:40 W |
| 额定电压:220 V |
| 频率:50 Hz |

(1)如果饮水机处在“加热”状态正常工作时,电热丝所产生的热量有80%被水吸收,饮水机的热胆装满水,水温由20℃加热到90℃,需用多长时间?
(2)开关断开时,饮水机处于 状态(填“加热”或“保温”)。
(3)电阻丝R1的阻值。
在真空中传播的波长是20 m的电磁波,进入某一介质中传播时,其传播速度为1×108 m/s,求此电磁波在介质中的波长.
如图所示,一列沿x轴正方向传播的简谐横波,波速大小为0.3 m/s,P点的横坐标为96 cm,从图中状态开始计时,求: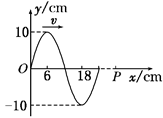
(1)经过多长时间,P质点开始振动,振动时方向如何?
(2)经过多长时间,P质点第一次到达波峰?
(3)以P质点第一次到达波峰开始计时,作出P点的振动图像(至少画出1.5个周期)
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,介质中质点P、Q分别位于x=2 m、x=4 m处.从t=0时刻开始计时,当t=15 s时质点Q刚好第4次到达波峰.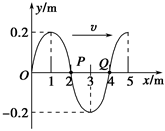
(1)求波速.
(2)写出质点P做简谐运动的表达式(不要求推导过程).
渔船常利用超声波来探测远处鱼群的方位.已知某超声波频率为1.0×105 Hz,某时刻该超声波在水中传播的波动图像如图所示.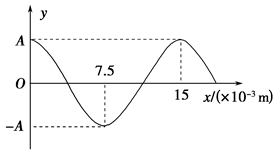
(1)从该时刻开始计时,画出x=7.5×10-3 m处质点做简谐运动的振动图像(至少一个周期).
(2)现测得超声波信号从渔船到鱼群往返一次所用时间为4 s,求鱼群与渔船间的距离(忽略船和鱼群的运动).
(14分)如图所示,一个光滑的圆弧形槽半径为R,放在水平地面上,圆弧所对的圆心角小于5°.AD的长为x,今有一小球m1以沿AD方向的初速度v从A点开始运动,要使小球m1可以与固定在D点的小球m2相碰撞,那么小球m1的速度v应满足什么条件?