冬季，养鸡场为了提高产蛋量，夜间需要在鸡舍里用电热器加热并用灯泡照明；白天只需要在鸡舍里用电热器加热，不需要用灯泡照明。小阳根据上述要求设计了一种加热照明装置，这个装置的电路图如图所示，电阻R1和R2是两个用来加热且阻值不变的电阻丝，灯L是标有“220V 160W”的照明灯泡，开关S1、S2的通断只有两种状态，一种是同时断开，另一种是同时闭合。该装置从早晨7:00至17:00处于白天工作状态，连续正常工作10h，这段时间内电流表的示数为5.5A，电阻R1的电功率为P1，电阻R2的电功率为P2，电路的总电功率为P；该装置从17:00至第二天早晨7:00处于夜间工作状态，连续正常工作14h。已知：电源两端的电压U恒为220V，
。求：
（1）总电功率P；
（2）电阻R2的阻值；
（3）从早晨7:00到第二天早晨7:00的24h内，该加热照明装置共消耗电能多少千瓦时。
如图所示，一轻绳上端系在车的左上角的A点，另一轻绳一端系在车左端B点，B点在A点正下方，A、B距离为b，两绳另一端在C点相结并系一质量为m的小球，绳AC长度为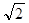
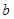，绳BC长度为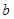。两绳能够承受的最大拉力均为
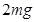。求：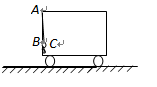
（1）绳BC刚好被拉直时，车的加速度是多大? （要求画出受力图）
（2）在不拉断轻绳的前提下，求车向左运动的最大加速度是多大?（要求画出受力图）
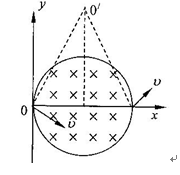
如图所示，圆形区域的匀强磁场，磁感应强度为B、方向垂直纸面向里，边界跟y轴相切于坐标原点O。 O点处有一放射源，沿纸面向各方向射出速率均为v的某种带电粒子，带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍。已知该带电粒子的质量为m、电量为q，不考虑带电粒子的重力。
（1）推导粒子在磁场空间做圆周运动的轨道半径；
（2）求粒子通过磁场空间的最大偏转角；
（3）若粒子与磁场边界碰撞后以原速率反弹，则从O点沿x轴正方向射入磁场的粒子第一次回到O点经历的时间是多长？（已知arctan2=
）
坐标原点O处有一点状的放射源，它向xoy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小都是v0，在0<y<d的区域内分布有指向y轴正方向的匀强电场，场强大小为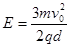
，其中q与m分别为α粒子的电量和质量；在d<y<2d的区域内分布有垂直于xoy平面的匀强磁场.ab为一块很大的平面感光板，放置于y=2d处，如图所示，.观察发现此时恰无粒子打到ab板上.（不考虑a粒子的重力）
（1）求α粒子刚进人磁场时的动能；
（2）求磁感应强度B的大小；
（3）将ab板平移到什么位置时所有粒子均能打到板上?并求出此时ab板上被α粒子打中的区域的长度.
如图所示，在直角坐标系O-xyz中存在磁感应强度为B=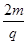
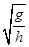，方向竖直向下的匀强磁场，在(0,0,h)处固定一电量为+q(q>0)的点电荷，在xOy平面内有一质量为m，电量为-q的微粒绕原点O沿图示方向做匀速圆周运动。若该微粒的圆周运动可以等效为环形电流，求此等效环形电流强度I。（重力加速度为g）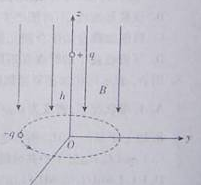
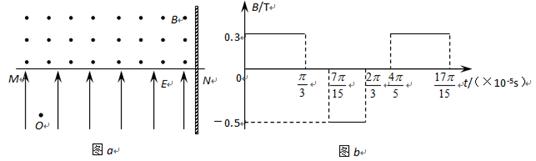
如图a所示，水平直线MN下方有竖直向下的匀强电场，现将一重力不计、比荷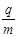
＝106C/kg的正电荷于电场中的O点由静止释放，经过
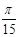×10-5 s时间以后电荷以v0＝1.5×104 m/s的速度通过MN进入其上方的均匀磁场，磁场与纸面垂直，磁感应强度B按图b所示规律周期性变化（图b中磁场以垂直纸面向外为正，以电荷第一次通过MN时为t=0时刻）。求：
（1）匀强电场的电场强度E；
（2）图b中t＝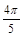
×10-5 s时刻电荷与O点的水平距离；
（3）如果在O点正右方d = 68cm处有一垂直于MN的足够大的挡板，求电荷从O点出发运动到挡板的时间。