下图是用传送带传送行李的示意图。图中水平传送带AB间的长度为8m,它的右侧是一竖直的半径为0.8m的1/4圆形光滑轨道,轨道底端与传送带在B点相切。若传送带向右以6m/s的恒定速度匀速运动,当在传送带的左侧A点轻轻放上一个质量为4kg的行李箱时,箱子运动到传送带的最右侧如果没被捡起,能滑上圆形轨道,而后做往复运动直到被捡起为止。已知箱子与传送带间的动摩擦因数为0.1,重力加速度大小为g=10m/s2,求:
⑴箱子从A点到B点所用的时间及箱子滑到圆形轨道底端时对轨道的压力大小;
⑵若行李箱放上A点时给它一个5m/s的水平向右的初速度,到达B点时如果没被捡
起,则箱子离开圆形轨道最高点后还能上升多大高度?在给定的坐标系中定性画出箱子从A点到最高点过程中速率v随时间t变化的图象。
“绿色奥运”是2008年北京奥运会的三大理念之一,奥组委决定在各比赛场馆使用新型节能环保电动车,届时江汉大学的500名学生将担任司机,负责接送比赛选手和运输器材。在检测某款电动车性能的某次实验中,质量为8×102㎏的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F— 图象(图中AB、BO均为直线))。假设电动车行驶中所受的阻力恒定,
图象(图中AB、BO均为直线))。假设电动车行驶中所受的阻力恒定,
求此过程中(1)电动车的额定功率;
(2)电动车由静止开始运动,经过多长时间,速度达到2m/s?
酒后驾车严重威胁交通安全。饮酒后会使人的反应时间(从发现情况到实施作制动的时间)变长,造成反制距离(从发现情况到汽车停止的距离)变长。假定汽车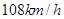 的速度匀速行驶,刹车时汽车的加速度大小是
的速度匀速行驶,刹车时汽车的加速度大小是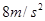 ,正常人的反应时间为
,正常人的反应时间为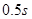 ,饮酒人的反应时间为
,饮酒人的反应时间为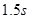 .
.
问:(1)驾驶员饮酒后的反制距离比正常时多几米?
(2)饮酒的驾驶员从发现情况到汽车停止需多少时间?
汽车从静止开始以a=1m/s2的加速度直线前进,车前与车相距x0=20m处,某人同时开始以4m/s的速度同方向匀速向前运动。
(1)经过多长时间汽车的速度达到4m/s?
(2)汽车追上人之前,他们之间的最大间距是多少?
(3)经过多长时间车才追上人?
某校一课外活动小组自制一枚火箭,设火箭发射后始终在垂直于地面的方向上运动.火箭点火后可认为做匀加速直线运动,经过4 s到达离地面40 m高处时燃料恰好用完,燃料用完后的运动认为是只受重力的竖直上抛下落运动,取g=10 m/s2,求:
(1)燃料恰好用完时火箭的速度;
(2)火箭上升离地面的最大高度;
(3)火箭从发射到残骸落回地面过程的总时间.
(1)某一猎豹在追逐猎物的过程中,运动时速达到20m/s,由于猎物的躲避,猎豹能在原野上滑行20米的距离急停,问:猎豹急停过程,花费的时间?
(2)一辆汽车在平直的高速公路上以108km/h的速度行驶,如果该辆汽车拥有该猎豹急停的加速度,则它从刹车开始,4秒内发生的位移的大小是多少米?