如图所示，竖直平面内有一固定的光滑椭圆大环，其长轴长BD=4L、短轴长AC=2L。劲度系数为k的轻弹簧上端固定在大环的中心0，下端连接一个质量为m、电荷量为q、可视为质点的小环，小环刚好套在大环上且与大环及弹簧绝缘，整个装置处在水平向右的匀强电场中。将小环从A点由静止释放，小环运动到B点时速度恰好为O。已知小环在A、 B两点时弹簧的形变量大小相等。则（ ）
A.小环从A点运动到B点的过程中，弹簧的弹性势能一直增大
B.小环从A点运动到B点的过程中，小环的电势能一直减小
C.电场强度的大小
D.小环在A点时受到大环对它的弹力大小
喷墨打印机的简化模型如图所示，重力可忽略的墨汁微滴，经带电室带负电后，以速度
垂直匀强电场飞入极板间，最终打在纸上，则微滴在极板间电场中（ ）
| A．电势能逐渐增大 |
| B．运动轨迹是抛物线 |
| C．运动轨迹与初速度无关 |
| D．运动轨迹与带电量无关 |
如图所示，A、B为两块竖直放置的平行金属板，G是静电计，开关S合上后，静电计指针张开一个角度．下述哪些做法可使指针张角增大（ ）
A．使A、B两板靠近些
B．使A、B两板正对面积错开些
C．断开S后，使A板向右平移些
D．断开S后，使A、B正对面积错开些
A、B是一条电场线上的两点，若在A点释放一初速度为零的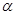
粒子（带正电），仅受电场力作用，并沿电场线从A运动到B，其速度随时间变化的规律如图所示．设A、B两点的电场强度分别为EA、EB，电势分别为φA、φB ，则( )
A.EA＝EB B.EA<EB C.φA>φB D.φA<φB
将一电荷量为+Q的小球放在不带电的金属球附近，所形成的电场线分布如图所示，金属球表面的电势处处相等．a、b为电场中的两点，则下列说法错误的是（ ）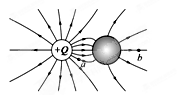
| A．a点的电场强度比b点的大 |
| B．a点的电势比b点的高 |
| C．检验电荷-q在a点的电势能比在b点的大 |
| D．将检验电荷-q从a点移到b点的过程中，电场力做负功 |
有一横截面积为S的铝导线，当有电压加在该导线上时，导线中的电流强度为I。设每单位体积的导线中有n个自由电子，电子电量为e，此时电子定向移动的速度为v，则在△t时间内，通过导体横截面的自由电子数目可表示为（）
A． |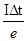
B．nvS | C．nv△t | D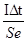． |