【2015·福建·22】如图,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B。一质量为m、电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑,到达C点时离开MN做曲线运动。A、C两点间距离为h,重力加速度为g。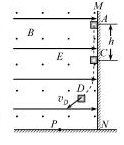
(1)求小滑块运动到C点时的速度大小vc;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点。已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vp.
在消防演习中,消防队员从一根竖直的长直轻绳上由静止滑下,经2.5s落地.为了获得演习中的一些数据,以提高训练质量,研究人员在轻绳上端安装一个力传感器并与数据处理系统相连接,用来记录消防队员下滑过程中轻绳受到的拉力与消防队员重力的比值随时间变化的情况.已知某队员在一次演习中的数据如图所示,求该消防队员在下滑过程中的最大速度和落地速度各是多少?(g取10m/s2)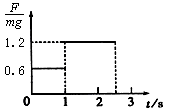
如图所示,光滑金属球的重力G=40 N.它的左侧紧靠竖直的墙壁,右侧置于倾角θ=37°的斜面体上。已知斜面体处于水平地面上保持静止状态,sin 37°=0.6,cos 37°=0.8.求:
(1)墙壁对金属球的弹力大小;
(2)水平地面对斜面体的摩擦力的大小和方向
一颗自由下落的小石头,经过某点时的速度是10 m/s,经过另一点时的速度是30 m/s, 求经过这两点的时间间隔和两点间的距离。(取g=10 m/s2)
(理科第三、第四、第五及第六、第七考场的学生做此题)
用相同钢珠从斜面上的某点每隔0.1s放下一颗,在连续放下几颗后,对于在斜面上运动的小钢珠摄得如图所示的相片,现测得AB=15cm,BC=20cm,
试求:
(1)钢珠运动的加速度;
(2)拍摄时B钢珠的速度;
(3)图中C、D钢珠间的距离;
(理科第一和第二两个考场的学生做此题)
用相同钢珠从斜面上的某点每隔0.1s放下一颗,在连续放下几颗后,对于在斜面上运动的小钢珠摄得如图所示的相片,现测得AB=15cm,BC=20cm,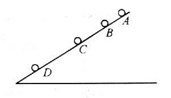
试求:
(1)钢珠运动的加速度;
(2)拍摄时B钢珠的速度;
(3)A钢珠上面正在运动的钢珠还有几颗?