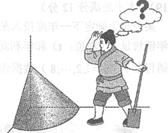
【2015高考新课标1,文6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )
A.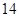 斛 斛 |
B.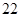 斛 斛 |
C.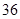 斛 斛 |
D. 斛 斛 |
用反证法证明“若x+y≤0则x≤0或y≤0”时,应假设()
| A.x>0或y>0 | B.x>0且y>0 |
| C.xy>0 | D.x+y<0 |
在△ABC中,已知a﹣b=4,a+c=2b,且最大角为120°,则这个三角形的最大边等于()
| A.4 | B.14 | C.4或14 | D.24 |
某产品的广告费用x与销售额y的统计数据如下表:
| 广告费用x(万元) |
3 |
4 |
5 |
6 |
| 销售额y(万元) |
25 |
30 |
40 |
45 |
根据上表可得回归方程 =
= x+
x+ ,其中
,其中 为7,据此模型,若广告费用为10万元,预报销售额等于()
为7,据此模型,若广告费用为10万元,预报销售额等于()
A.42.0万元B.57.0万元
C.66.5万元D.73.5万元
已知x,y∈R,则(x2+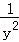 )(
)(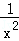 +4y2)的最小值为()
+4y2)的最小值为()
| A.10 | B.8 | C.9 | D.7 |
满足2n﹣1<(n+1)2的最大正整数n的取值是()
| A.6 | B.7 | C.8 | D.9 |