【2015高考上海,理23】对于定义域为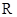 的函数
的函数 ,若存在正常数
,若存在正常数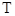 ,使得
,使得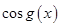 是以
是以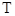 为周期的函数,则称
为周期的函数,则称 为余弦周期函数,且称
为余弦周期函数,且称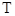 为其余弦周期.已知
为其余弦周期.已知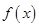 是以
是以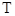 为余弦周期的余弦周期函数,其值域为
为余弦周期的余弦周期函数,其值域为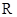 .设
.设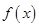 单调递增,
单调递增, ,
, .
.
(1)验证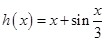 是以
是以 为周期的余弦周期函数;
为周期的余弦周期函数;
(2)设 .证明对任意
.证明对任意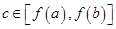 ,存在
,存在 ,使得
,使得 ;
;
(3)证明:“ 为方程
为方程 在
在 上得解”的充要条件是“
上得解”的充要条件是“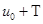 为方程
为方程 在
在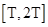 上有解”,并证明对任意
上有解”,并证明对任意 都有
都有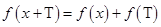 .
.
如图,A,B是海面上位于东西方向相距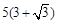 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距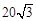 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
数列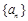 的通项公式为
的通项公式为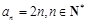 ,等比数列
,等比数列 满足
满足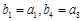 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前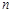 项和
项和 ;
;
(3)设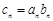 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知在△ABC中,若角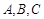 所对的边分别为
所对的边分别为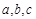 ,且
,且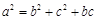 .
.
(1)求角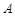 的大小;
的大小;
(2)若 ,求边
,求边 的值.
的值.
已知在等差数列 中,
中, .
.
(1)求通项公式 ;
;
(2)求前 项和
项和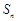 的最大值.
的最大值.
已知抛物线 ,直线
,直线 ,
, 是抛物线的焦点。
是抛物线的焦点。
(1)在抛物线上求一点 ,使点
,使点 到直线
到直线 的距离最小;
的距离最小;
(2)如图,过点 作直线交抛物线于A、B两点.
作直线交抛物线于A、B两点.
①若直线AB的倾斜角为 ,求弦AB的长度;
,求弦AB的长度;
②若直线AO、BO分别交直线 于
于 两点,求
两点,求 的最小值.
的最小值.