（本题12分）如图，直线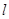
：
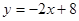分别与
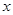轴、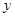
轴交于A、B两点，点C线段AB上，作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE；
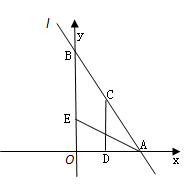
（1）填空：点C的坐标为（ ， ）；点E的坐标为（ ， ）；
（2）直线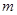
过点E，且将△AOB分成面积比为1：2的两部分，求直线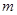的表达式；
（3）点P在x轴上运动，
①当PC+PE取最小值时，求点P的坐标及PC+PE的最小值；
②当PC-PE取最大值时，求点P的坐标及PC-PE的最大值；
如图，▱ABCD中，点E、F分别在边AD、BC上，且AE=CF，连接BE、DF．求证：BE∥DF．
将正比例函数y=2x的图象沿y轴平移后，恰好经过点A（2，3），求平移后的函数解析式．
如图，直线y=﹣
x+1交y轴于A点，交x轴于C点，以A，O，C为顶点作矩形AOCB，将矩形AOCB绕O点逆时针旋转90°，得到矩形DOFE，直线AC交直线DF于G点．
（1）求直线DF的解析式；
（2）求证：OG平分∠CGD；
（3）在第一象限内，是否存在点H，使以G，O，H为顶点的三角形为等腰直角三角形？若存在请求出点H的坐标；若不存在，请什么理由．
如图1，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，BF∥DE且交AG于点F．
（1）求证：AE=BF；
（2）如图2，连接DF、CE，探究线段DF与CE的关系并证明；
（3）图1中，若AB=4，BG=3，求EF长．
将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F，
（1）求证：四边形AECF为菱形；
（2）若AB=4，BC=8，求菱形的边长；
（3）在（2）的条件下折痕EF的长．