阅读理解:
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.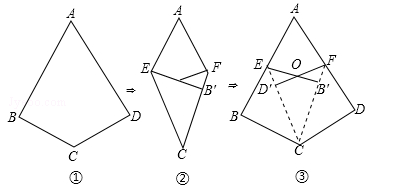
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图③中的∠BCD=120°时,∠AEB′= °;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有 个(包含四边形ABCD).
拓展提升:
(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.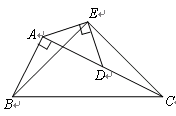
小明家、王老师家、学校依次在同一条路上.小明家到王老师家的路程为3千米,王老师家到学校的路程为0.5千米.由于小明的父母在外地工作,为了使小明能按时到校,王老师每天骑自行车接小明上学.已知王老师骑自行车的速度是步行速度的3倍,接小明上学时每天比平时步行上班多用了20分钟.问王老师的步行速度及骑自行车的速度各是多少?
解不等式组,并将其解集在数轴上表示出来.
国家个人所得税法规定,月收入不超过1600元的不纳锐,月收入超过1600元的部分按照下表规定的税率缴纳个人所得税:
| 全月应纳税所得额 |
税率(%) |
| 不超过500元的部分 |
5 |
| 超过500~2000元的部分 |
10 |
| 超过2000~5000元的部分 |
15 |
| … |
… |
试写出在不同段的工资所缴纳的个人所得税.(设工资为x元,0<x≤5 000)
某校暑假将组织该校“三好学生”去北京旅游,由3名老师带队,甲旅行社说:“如果带队老师买全票,则其余学生可享受半价优惠”,乙旅行社说:“包括带队老师在内全部按全票价的6折优惠”.若全票价是800元,设学生数为x人,分别计算两家旅行社的收费.