如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15cm，CD=20cm，AB和CD之间有一景观池，小南在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°（点B、E、D在同一直线上），求两幢建筑物之间的距离BD（结果精确到0.1m）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）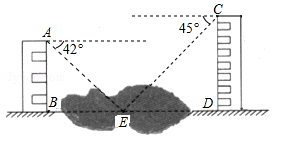
校车安全是近几年社会关注的重大问题，安全隐患主要是超载和超速.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道
上确定点D，使CD与垂直，测得CD的长等于21米，在上点D的同侧取点A、B，使∠CAD=30°，∠CBD =60°
(1)求AB的长（精确到0.1米，参考数据：
，
）；
(2)已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由.
有两个不同形状的计算器（分别记为A，B）和与之匹配的保护盖（分别记为a，b）（如图所示）散乱地放在桌子上．
（1）若从计算器中随机取一个，再从保护盖中随机取一个，求恰好匹配的概率．
（2）若从计算器和保护盖中随机取两个，用树形图法或列表法，求恰好匹配的概率．
“初中生骑电动车上学”的现象越来越受到社会的关注，某校利用“五一”假期，随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法，统计整理制作了如下的统计图，请回答下列问题：
⑴这次共抽查了个家长；
⑵请补全条形统计图和扇形统计图（友情提醒：条形图补画家长持“反对”态度的人数条，扇形图填上“反对”及“赞成”的百分数）；
⑶已知该校共有1200名学生，持“赞成”态度的学生估计约有人．
如图，在
ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．求证：BE=DF．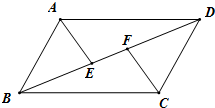
（1）解方程：
（2）解不等式组：