(12分)如图（a）所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度为B；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放。在ab棒运动到区域Ⅱ的下边界EF处之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为2l，在t=tx时刻（tx未知）ab棒恰进入区域Ⅱ，重力加速度为g。求：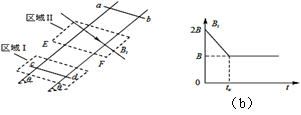
（1）通过cd棒电流的方向和区域I内磁场的方向；
（2）当ab棒在区域Ⅱ内运动时，cd棒消耗的电功率；
（3）ab棒开始下滑的位置离EF的距离；
（4）ab棒开始下滑至EF的过程中回路中产生的热量。
如图所示，一带电为+q质量为m的小球，从距地面高h处以一定的初速水平抛出，在距抛出点水平距离为L处有根管口比小球略大的竖直细管，管的上口距地面h/2。为了使小球能无碰撞地通过管子（即以竖直速度进入管子），可在管子上方整个区域内加一水平向左的匀强电场，（重力加速度为g）求：
（1）小球的初速度
(2）应加电场的场强
（3）小球落地时的动能
如图所示，电解槽A与电炉R并联后接到电源上，电源内阻r =1Ω，电炉电阻R=19Ω，电解槽接入电路中的电阻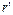
=0.5Ω．当K1闭合、K2断开时，电炉消耗功率684W；K1、K2都闭合时电炉消耗功率475W（电炉电阻可看作不变）．试求
（1）电源的电动势；
（2）K1、K2闭合时，流过电解槽的电流大小；
（3）K1、K2闭合时，电解槽中电能转化成化学能的功率。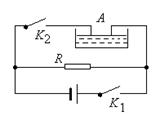
如
图所示,电源电动势E=2V,内电阻r=0.5Ω,竖直平面内的导轨电
阻可忽略,金属棒的质量m=0.1kg,电阻R=0.5Ω,它与导轨间的动摩擦因数µ=0.4,有效长度为L=0.2m.为了使金属棒能够靠在竖直导轨外面静止不动,我们施加一竖直方向的匀强磁场,问磁场方向是向上还是向下?磁感应强度B至少应是多大?设滑动摩擦力等于最大静摩擦力。（重力加速度g=10m/s2）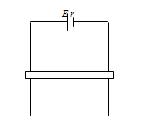
有一游标卡尺，主尺的最小分度是1mm，游标上有20个小的等分刻度。用它测量一小球的直径，如图甲所示的读数是mm。用螺旋测微器测量一根金属丝的直径，如图乙所示的读数是mm。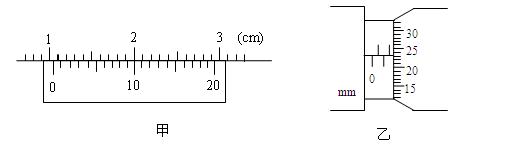
如图所示两个质量分别为M1、M2的劈A、B，高度相同。放在光滑水平面上，A、B的上表面为光滑曲面，曲面末端与地面相切。有一质量为m的物块（可视为质点）自劈顶端自由下滑。劈顶端到地面距离h=0.06m，劈A与物块的质量比M1/m =5。
求：（I）物块离开A瞬间A和物块的速度各多大？(g=10m/s2)
（II）物块从A上滑下后又冲上B，若要保证物块离开B后不能追上A，则B与物块的质量比M2/m应满足什么条件。