在平面直角坐标系中,O为原点,四边形OABC的顶点A在 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥ 轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出 的取值范围.
的取值范围.
(12分)已知数列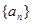 的首项为
的首项为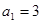 ,通项
,通项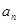 与前n项和
与前n项和 之间满足
之间满足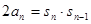 (n≥2)。 (1)求证:
(n≥2)。 (1)求证: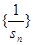 是等差数列,并求公差; (2)求数列
是等差数列,并求公差; (2)求数列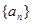 的通项公式。
的通项公式。
(12分)锐角三角形ABC的内角A,B,C的对边分别为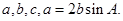
(1)求B的大小;(2)求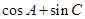 的取值范围.
的取值范围.
(12分) 已知函数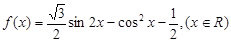
(1)当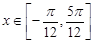 时,求函数
时,求函数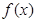 的最大值;(2)设
的最大值;(2)设 的内角
的内角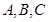 的对应边分别为
的对应边分别为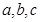 ,且
,且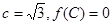 ,若向量
,若向量 与向量
与向量 共线,求
共线,求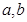 的值.
的值.
(12分)已知函数f(x)=cos(2x-)+2sin(x-)sin(x+).
(1)求函数f(x)的最小正周期; (2)求函数f(x)在区间[-,]上的值域.
.设函数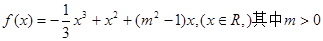
(Ⅰ)当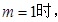 曲线
曲线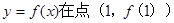 处的切线斜率
处的切线斜率
(Ⅱ)求函数的单调区间与极值;
(Ⅲ)已知函数 有三个互不相同的零点0,
有三个互不相同的零点0,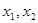 ,且
,且 。若对任意的
。若对任意的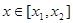 ,
,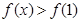 恒成立,求m的取值范围。
恒成立,求m的取值范围。