已知向量a,b, |a|=6,|b|=8,且|a+b|=|a-b|,求|a-b|.
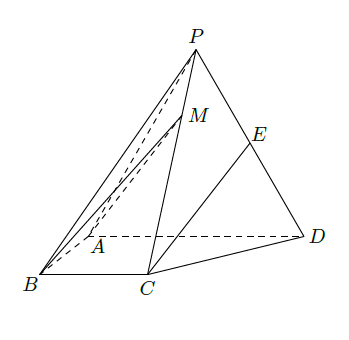
如图,四棱锥
中,侧面
为等比三角形且垂直于底面
,
是
的中点.
(1)证明:直线 平面 ;
(2)点 M在棱 PC上,且直线 BM与底面 ABCD所成锐角为 ,求二面角 的余弦值.
淡水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg)某频率直方图如下:
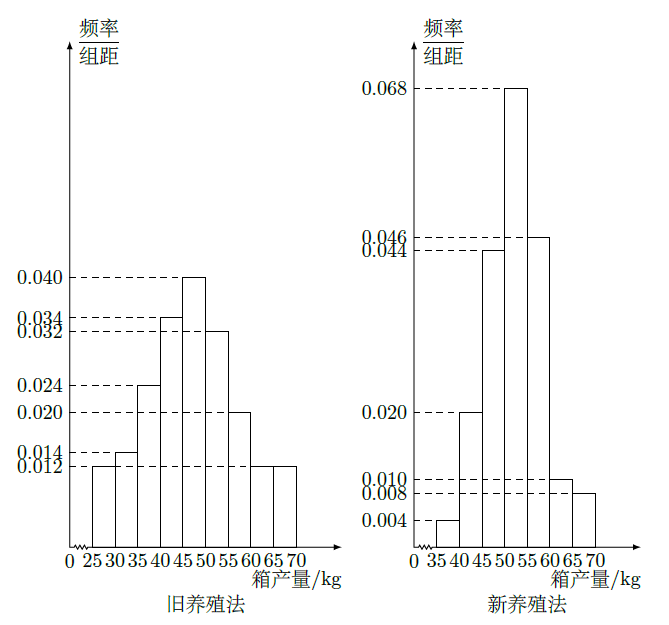
(1)设两种养殖方法的箱产量相互独立,记A表示事件:旧养殖法的箱产量低于50kg, 新养殖法的箱产量不低于50kg,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
|
箱产量<50kg |
箱产量≥50kg |
|
|
旧养殖法 |
||
|
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01)
|
P( |
0.050 |
0.010 |
0.001 |
|
k |
3.841 |
6.635 |
10.828 |
的内角
的对边分别为
,已知
.
(1)求
(2)若 , 面积为2,求
已知椭圆
的左焦点为
,右顶点为A,点E的坐标为(0,c),
的面积为
.
(I)求椭圆的离心率;
(II)设点Q在线段AE上, ,延长线段FQ与椭圆交于点P,点M,N在x轴上, ,且直线PM与直线QN间的距离为c,四边形PQNM的面积为3c.
(i)求直线FP的斜率;
(ii)求椭圆的方程.
设a,
,
.已知函数
,
.
(Ⅰ)求 的单调区间;
(Ⅱ)已知函数 和 的图象在公共点 处有相同的切线,
(i)求证: 处的导数等于0;
(ii)若关于x的不等式 在区间 上恒成立,求b的取值范围.