如图,已知圆 ,动直线
,动直线 过点
过点 交圆
交圆 于
于 ,
, 两点(点
两点(点 在
在 轴上方),点
轴上方),点 在
在 轴上,若点
轴上,若点 的坐标为
的坐标为 ,则点
,则点 的横坐标为
的横坐标为 .
.
(1)求 的值;
的值;
(2)当直线 的斜率为
的斜率为 时,直线
时,直线 与圆
与圆 相切,求点
相切,求点 的坐标;
的坐标;
(3)试问:是否存在一定点 ,使得
,使得 总成立?若存在,请求出点
总成立?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知命题p方程2x2+ax﹣a2=0在[﹣1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p∨q”是假命题,求实数a的取值范围.
已知函数 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值及函数f(x)的单调递增区间;
(Ⅱ)当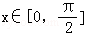 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
已知函数
(Ⅰ)求函数f(x)的定义域
(Ⅱ)若 ,求cosα的值
,求cosα的值
(Ⅲ)在(Ⅱ)条件下,若α是第四象限角,求 的值.
的值.
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=3,直线l的参数方程为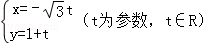 .试在曲线C上求一点M,使它到直线l的距离最大.
.试在曲线C上求一点M,使它到直线l的距离最大.
已知函数f(x)=x2﹣(a+2)x+alnx.
(1)当a=1时,求函数f(x)的极值;
(2)设定义在D上的函数y=g(x)在点P(x0,y0)处的切线方程为l:y=h(x).当x≠x0时,若 >0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,问函数y=f(x)是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,问函数y=f(x)是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.