若存在实常数 和
和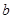 ,使得函数
,使得函数 和
和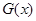 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和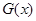 的“隔离直线”,已知函数
的“隔离直线”,已知函数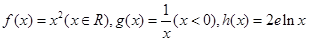 ,有下列命题:
,有下列命题:
① 在
在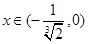 内单调递增;
内单调递增;
②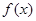 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且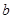 的最小值为
的最小值为 ;
;
③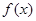 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是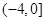 ;
;
④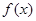 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( )
A. 个 个 |
B.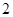 个 个 |
C. 个 个 |
D. 个 个 |
若一个几何体的主视图和侧视图都是等腰梯形,则这个几何体可能是
| A.圆柱 | B.棱锥 | C.球体 | D.圆台 |
直线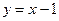 与抛物线
与抛物线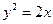 相交于P、Q两点,抛物线上一点M与P、Q构成
相交于P、Q两点,抛物线上一点M与P、Q构成 MPQ的面积为
MPQ的面积为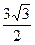 ,这样的点M有且只有()个
,这样的点M有且只有()个
| A.1 | B.2 | C.3 | D.4 |
在正三棱柱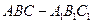 中,
中,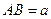 ,D、E分别是BB1、CC1上的点,满足BC=EC=2BD,则平面ABC与平面ADE所成的二面角的大小为()
,D、E分别是BB1、CC1上的点,满足BC=EC=2BD,则平面ABC与平面ADE所成的二面角的大小为()
A、30° B、45° C、60° D、75°
与双曲线 有共同渐近线,且经过点(-3,
有共同渐近线,且经过点(-3, )的双曲线的一个焦点到一条渐近线的距离为()
)的双曲线的一个焦点到一条渐近线的距离为()
| A.8 | B.4 | C.2 | D.1 |
如图,在正三棱柱 中,已知AB=1,D在棱BB1上,
中,已知AB=1,D在棱BB1上,
且BD=1,若AD与平面AA1C1C的所成角为 ,则
,则 =()
=()
A.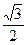 |
B.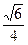 |
C. |
D.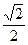 |
|