（本题12分）类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”。
（1）概念理解
如图1，在四边形ABCD中，添加一个条件，使得四边形ABCD是“等邻边四边形”，请写出你添加的一个条件；
（2）问题探究
①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由；
②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠B的平分线BB’方向平移得到△A’B’C’，连结AA’，BC’。小红要使平移后的四边形ABC’A’是“等邻边四边形”，应平移多少距离（即线段BB’的长）？
（3）应用拓展
如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC，BD为对角线，AC=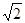
AB。试探究BC，CD，BD的数量关系。
（本题6分）一次函数
的图象经过点A（−3，−2）．
（1）求这个一次函数的关系式；
（2）判断点B（-5，3）是否在这个函数的图象上．
在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线， DE⊥AB于点E．
（1）如图1，连接EC，求证：△EBC是等边三角形；
（2）点M是线段CD上的一点（不与点C，D重合），以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G．请你在图2中画出完整图形，并直接写出MD，DG与AD之间的数量关系；
（3）如图3,点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G．试探究ND，DG与AD数量之间的关系，并说明理由．
在平面直角坐标系中，P点坐标为（2，6），Q点坐标为（2,2），点M为y轴上的动点.
（1）在平面直角坐标系内画出当△PMQ的周长取最小值时点M的位置（保留作图痕迹）；
（2）写出点M的坐标__________________.
如图：
中，
，AM是BC边上的中线，点N在AM上.求证：
.
列方程解应用题：
为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场．现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两个工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品.