如图1，在平面直角坐标系中，抛物线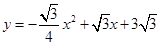
交
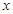轴于A，B两点（点A在点B的左侧），交
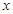轴于点W，顶点为C，抛物线的对称轴与轴的交点为D。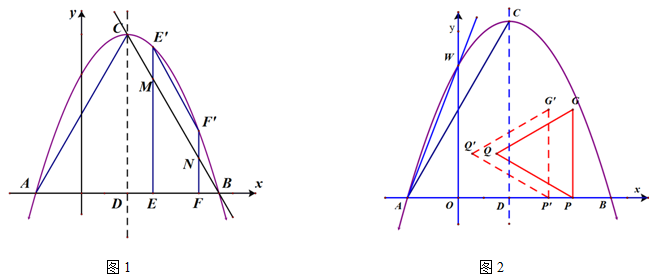
（1）求直线BC的解析式；
（2）点E（m，0），F（m+2，0）为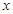轴上两点，其中
，
，
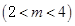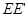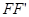分别垂直于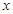轴，交抛物线与点
，
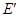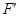，交BC于点M，N，当
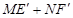的值最大时，在轴上找一点R，使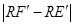
的值最大，请求出R点的坐标及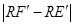的最大值；
（3）如图2，已知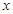轴上一点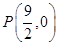
，现以P为顶点，
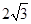为边长在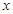轴上方作等边三角形QPG，使GP⊥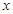轴，现将△QPG沿PA方向以每秒1个单位长度的速度平移，当点P到达点A时停止，记平移后的△QPG为
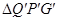，设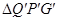与△ADC的重叠部分面积为s，当点
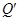到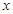轴的距离与点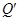到直线AW的距离相等时，求s的值。
n2；