（满分14分）如图，抛物线经过
（
），
（
），
（
）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点
，使
的值最小，求点的坐标；
（3）点
为
轴上一动点，在抛物线上是否存在点
，使得以
四点为顶点的四边形为平行四边形？若存在，请直接写出点的坐标．
有100米长的篱笆材料，想围成一个矩形露天仓库，要求面积不小于600平方米，在场地的北面有一堵长为50米的旧墙，有人用这个篱笆围成一个长40米，宽10米的矩形仓库，但面积只有400平方米，不合要求，现请你设计矩形仓库的长和宽，使它符合要求．
如图，某建筑工程队利用一面墙（墙的长度不限），用40米长的篱笆围成一个长方形的仓库．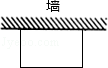
（1）求长方形的面积是150平方米，求出长方形两邻边的长；
（2）能否围成面积220平方米的长方形？请说明理由．
已知x1、x2是一元二次方程2x2﹣2x+m+1=0的两个实根．
（1）求实数m的取值范围；
（2）如果m满足不等式7+4x1x2＞x12+x22，且m为整数．求m的值．
已知方程2（m+1）x2+4mx+3m=2，根据下列条件之一求m的值．
（1）方程有两个相等的实数根；
（2）方程有两个相反的实数根；
（3）方程的一个根为0．
(6分)如图，△ABC中，AB=AC，∠BAC=45°，BD⊥AC，垂足为D点，AE平分∠BAC，交BD于F，交BC于E，点G为AB的中点，连接DG，交AE于点H，
（1）求∠ACB的度数；
（2）HE=
AF．