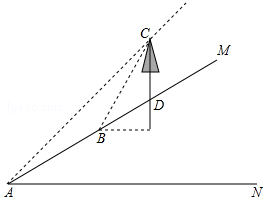
温岭是受台风影响较为严重的城市之一.如图,坡上有一颗与水平面EF垂直的大树AB,台风过后,大树倾斜后折断倒在山坡上,大树顶部B接触到坡面上的D点.已知山坡的坡角∠AEF=30°,量得树干倾斜角∠BAC=45°,大树被折断部分和坡面所成的角∠ADC=60°且AD=4米.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度AB.(结果精确到个位,参考数据: ≈1.4,
≈1.4, ≈1.7,
≈1.7, ≈2.4)
≈2.4)
(·辽宁朝阳)如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,你选择的条件是 (只填写序号).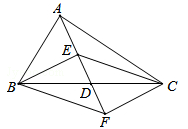
(·辽宁锦州)如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: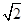 ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)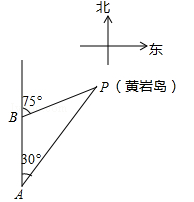
(·辽宁锦州)如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=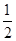 AB,连接EF,判断四边形ADEF的形状,并加以证明.
AB,连接EF,判断四边形ADEF的形状,并加以证明.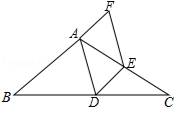
(·辽宁本溪)如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)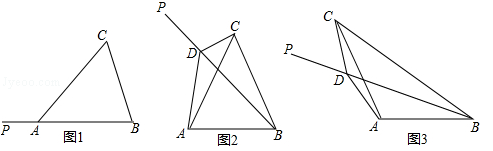
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=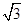 AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
(·辽宁本溪)张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据: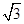 ≈1.732)
≈1.732)