如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多 少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
1 号 号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
89 |
100 |
95 |
119 |
97 |
500 |
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题计算两个班这五名学生的优秀率。
计算两个班这五名学生比赛数据的方差哪一个小
通过上面的计算你认为应该定哪一个班为冠军更合适?请你说明你的理由
如图,△ABC中,AB=AC,E,D分别是AB,AC上的点,连接BD,CE.请你增加一个条件(不再添加其它线段,不再标注其它字母),使BD=CE,并加以证明.
你添加的条件是:________________________________.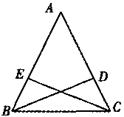
某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.符合题意的组建方案有几种?请你帮学校设计出来
若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,
试说明(1)中哪种方案费用最低,最低费用是多少元?
某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,
∠B=90º,AB =3m,BC=4m,AD=12m,CD=13m,若每种植1平方米草皮需要100元,问总共需要投入多少元?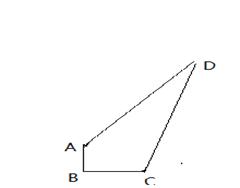
现有大小两艘轮船,小船每天运 x吨货物,大船比小船每天多运10吨货物.现在让大船完成运送100吨货物的任务,小船完成运送80吨货物的任务分别写出大船、小船完成任务用的时间?
试说明哪艘轮船完成任务用的时间少?