如图，抛物线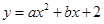
与坐标轴交于A、B、C三点，其中B（4，0）、C（﹣2，0），连接AB、AC，在第一象限内的抛物线上有一动点D，过D作DE⊥x轴，垂足为E，交AB于点F．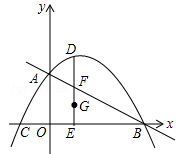
（1）求此抛物线的解析式；
（2）在DE上作点G，使G点与D点关于F点对称，以G为圆心，GD为半径作圆，当⊙G与其中一条坐标轴相切时，求G点的横坐标；
（3）过D点作直线DH∥AC交AB于H，当△DHF的面积最大时，在抛物线和直线AB上分别取M、N两点，并使D、H、M、N四点组成平行四边形，请你直接写出符合要求的M、N两点的横坐标．
如图所示，点E、F、G、H分别为□ABCD的边AB、BC、CD、DA的中点.求证：EF=HG.
先化简，再求值：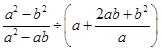
，其中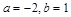
计算：
已知：正方形OABC的边OC、OA分别在x、y轴的正半轴上，设点B（4，4），点P（t，0）是x轴上一动点，过点O作OH⊥AP于点H，直线OH交直线BC于点D，连AD。
（1）如图1，当点P在线段OC上时，求证：OP=CD；
（2）在点P运动过程中，△AOP与以A、B、D为顶点的三角形相似时，求t的值；
（3）如图2，抛物线y=－x2+x+4上是否存在点Q，使得以P、D、Q、C为顶点的四边形为平行四边形，若存在，请求出t的值；若不存在，请说明理由。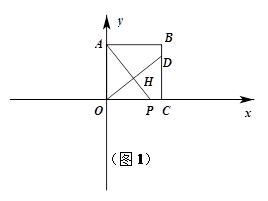
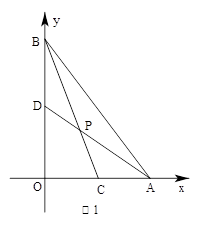
已知：点A、B分别在直角坐标系的x、y轴的正半轴上，O是坐标原点，点C在射线AO上，点D在线段OB上，直线AD与线段BC相交于点P，设=a， =b，=k。
（1）如图1，当a=，b=1时，请求出k的值；
（2）当a=，b=1时(如图2)，请求出k的值；当a=，b=时，k=▲；
（3）根据以上探索研究，请你解决以下问题：①请直接写出用含a，b代数式表示k=▲；② 若点A(8,0)，点B（0，6），C（－2，0），直线AD为：y=－x+4，则k=▲。
