天水“伏羲文化节”商品交易会上，某商人将每件进价为8元的纪念品，按每件9元出售，每天可售出20件．他想采用提高售价的办法来增加利润，经实验，发现这种纪念品每件提价1元，每天的销售量会减少4件．
（1）写出每天所得的利润y（元）与售价x（元/件）之间的函数关系式．
（2）每件售价定为多少元，才能使一天所得的利润最大？最大利润是多少元？
已知：△ABC中，∠A＝90°，AB＝AC，D为BC的中点，
（1）如图，E，F分别是AB，AC上的点，且BE＝AF，求证：△DEF为等腰直角三角形；
（2）若E，F分别为AB，CA延长线上的点，仍有BE＝AF，其他条件不变，那么，△DEF是否仍为等腰直角三角形？证明你的结论．
如图所示，直线
与
分别表示一种白炽灯和一种节能灯的费用y（费用=灯的售价+电费，单位：元）与照明时间x（h）的函数关系图像，假设两种灯的使用寿命都是2000h，照明效果一样． 
（1）根据图像分别求出L1，L2的函数关系式．
（2）当照明时间为多少时，两种灯的费用相等？
（3）小亮房间计划照明2500h，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法．
在平面直角坐标系中，A（－1，5），B（－2，1），C（－4，3）
（1）在图中作出△ABC关于y轴的对称图形△A1B1C1；
（2）写出点A1，B1，C1的坐标；
（3）求出△ABC的面积.
如图，已知AC∥DF，且BE=CF.
（1）请你只添加一个条件，使△ABC≌△DEF，你添加的条件是___________________；
（2）添加条件后，证明△ABC≌△DEF.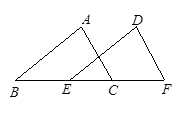
一次函数的图象经过A（3，5）和B（-4，-9）.
（1）求这个函数的解析式；
（2）若点（a，2）在该函数的图象上，试求a的值。