直线EF、GH之间有一个直角三角形ABC，其中∠BAC = 90°，∠ABC =
．
（1）如图1，点A在直线EF上，B、C在直线GH上，若∠=60°，∠FAC =30°．求证：EF∥GH;
（2）将三角形ABC如图2放置，直线EF∥GH，点C 、B分别在直线EF、GH上，且BC平分∠ABH，直线CD平分∠FCA交直线GH于D．在取不同数值时，∠BCD的大小是否发生变化？若不变求其值，若变化指出其变化范围．
如图，点O是线段AB上的一点，OA=OC，OD平分∠AOC交AC于点D，OF平分∠COB，CF⊥OF于点F．
（1）求证：四边形CDOF是矩形；
（2）当∠AOC多少度时，四边形CDOF是正方形？并说明理由．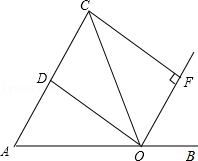
甲、乙两名运动员在相同的条件下各射靶10次，每次射靶的成绩情况如图所示：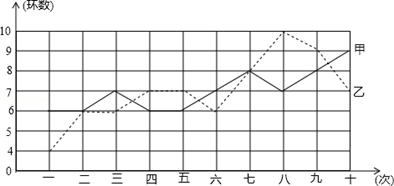
（1）请你根据图中数据填写下表：
| 运动员 |
平均数 |
中位数 |
方差 |
| 甲 |
7 |
7 |
|
| 乙 |
7 |
2.6 |
（2）根据以上信息分析谁的成绩好些．
如图，王强同学在甲楼楼顶A处测得对面乙楼楼顶D处的仰角为30°，在甲楼楼底B处测得乙楼楼顶D处的仰角为45°，已知甲楼高26米，求乙楼的高度．（
≈1.7）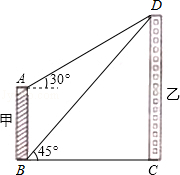
如图所示，在△ABC中，∠ABC=∠ACB．
（1）尺规作图：过顶点A作△ABC的角平分线AD；（不写作法，保留作图痕迹）
（2）在AD上任取一点E，连接BE、CE．求证：△ABE≌△ACE．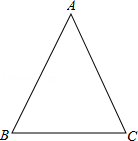
（1）计算：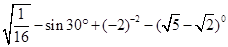
；
（2）求不等式组
的整数解．