选做题:从甲乙两题中选作一题,如果两题都做,只以甲题计分
题甲:已知矩形两邻边的长 、
、 是方程
是方程 的两根.
的两根.
(1)求 的取值范围;
的取值范围;
(2)当矩形的对角线长为 时,求
时,求 的值;
的值;
(3)当 为何值时,矩形变为正方形?
为何值时,矩形变为正方形?
题乙:如图, 是
是 直径,
直径, 于点
于点 ,交
,交 于
于
点 ,且
,且 .
.
(1)判断直线 和
和 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)当 ,
, 时,求
时,求 的面积.
的面积.
如图,在航线 的两侧分别有观测点
的两侧分别有观测点 和
和 ,点
,点 到航线
到航线 的距离为
的距离为 ,点
,点 位于点
位于点 北偏东
北偏东 方向且与
方向且与 相距
相距 处. 现有一艘轮船正沿该航线自西向东航行,在
处. 现有一艘轮船正沿该航线自西向东航行,在 点观测到点
点观测到点 位于南偏东
位于南偏东 方向,航行
方向,航行 分钟后,在
分钟后,在 点观测到点
点观测到点 位于北偏东
位于北偏东 方向.
方向.
(1)求观测点 到航线
到航线 的距离;
的距离;
(2)该轮船航线的速度(结果精确到 )
)
参考数据: ,
, ,
, ,
, ,
, ,
, ,
, .
.
如图,某地区对某种药品的需求量 (万件)、供应量
(万件)、供应量 (万件)与价格
(万件)与价格 (元/件)分别近似满足下列函数关系式:
(元/件)分别近似满足下列函数关系式: ,
, .需求量为
.需求量为 时,即停止供应. 当
时,即停止供应. 当 时,该药品的价格称为稳定价格,需求量称为稳定需求量.
时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该药品的稳定价格与稳定需求量;
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加 万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.
万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.
某货运码头,有稻谷和棉花共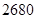 吨,其中稻谷比棉花多
吨,其中稻谷比棉花多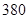 吨.
吨.
(1)求稻谷和棉花各是多少吨?
(2)现安排甲、乙两种不同型号的集装箱共 个,将这批稻谷和棉花运往外地.已知稻谷
个,将这批稻谷和棉花运往外地.已知稻谷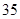 吨和棉花
吨和棉花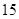 吨可装满一个甲型集装箱;稻谷
吨可装满一个甲型集装箱;稻谷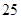 吨和棉花
吨和棉花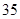 吨可装满一个乙型集装箱.在
吨可装满一个乙型集装箱.在 个集装箱全部使用的情况下,如何安排甲、乙两种集装箱的个数,有哪几种方案?
个集装箱全部使用的情况下,如何安排甲、乙两种集装箱的个数,有哪几种方案?
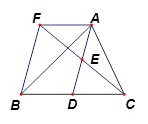
如图, 在 中,
中,  是
是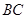 边上的一点,
边上的一点, 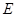 是
是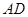 的中点, 过
的中点, 过 点作
点作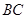 的平行线交
的平行线交 的延长线于点
的延长线于点 , 且
, 且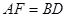 , 连接
, 连接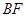 .
.
(1) 求证:  是
是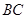 的中点;
的中点;
(2) 若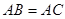 , 试判断四边形
, 试判断四边形 的形状, 并证明你的结论.
的形状, 并证明你的结论.