某校学生会准备调查2014-2015学年八年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数．
（1）确定调查方式时，甲同学说：“我到2014-2015学年八年级（1）班去调查全体同学”；乙同学说：“放学时我倒校门口随机调查部分同学”；丙同学说：“我到2014-2015学年八年级每个班随机调查一定数量的同学”．则调查方式最合理的是 同学．
（2）他们采用了最合理的调查方法收集数据，并绘制了下表和扇形统计图．
| 类别 |
频数 |
百分比 |
| 武术类 |
|
25% |
| 书画类 |
20 |
20% |
| 棋牌类 |
15 |
b |
| 器乐类 |
|
|
| 合计 |
a |
100% |
请你根据图表中提供的信息解答下列问题：
①求a、b的值；
②在扇形统计图中，求“器乐类”所对应扇形的圆心角的度数．
在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只能选两人打第一场．
（1）如果确定小亮打第一场，再从其余三人中随机选取一人打第一场，求恰好选中大刚的概率；
（2）如果确定小亮做裁判，用“手心、手背”的方法决定其余三人哪两人打第一场．游戏规则是：三人同时伸“手心、手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始，这三人伸出“手心”或“手背”都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率．
如图，在△ABC中，AB=BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．
求证：四边形BECD是矩形．
已知反比例函数y=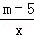
（m为常数，且m≠5）．
（1）若在其图象的每个分支上，y随x的增大而增大，求m的取值范围；
（2）若其图象与一次函数y=﹣x+1图象的一个交点的纵坐标是3，求m的值．
在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（﹣3，﹣1）．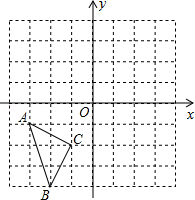
（1）将△ABC沿y轴正方向平移3个单位得到△A1B1C1，画出△A1B1C1，并写出点B1坐标；
（2）画出△A1B1C1关于y轴对称的△A2B2C2，并写出点C2的坐标．
解方程组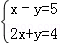
．