（1）如图1，将直角的顶点E放在正方形ABCD的对角线AC上，使角的一边交CD于点F，另一边交CB或其延长线于点G，求证：EF=EG；
（2）如图2，将（1）中的“正方形ABCD”改成“矩形ABCD”，其他条件不变．若AB=m，BC=n，试求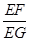
的值；
（3）如图3，将直角顶点E放在矩形ABCD的对角线交点，EF、EG分别交CD与CB于点F、G，且EC平分∠FEG．若AB=2，BC=4，求EG、EF的长．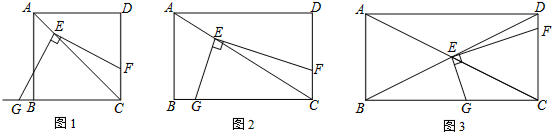
请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于65分，则本题的5个小题得分将计入全卷总分，但计入后全卷总分不超过65分；如果你全卷得分已经达到或超过65分，则本题可不做，得分不计入全卷总分．
（1）计算：（﹣2）+（﹣3）=，（﹣2）×5=，（﹣3）2=；
（2）用计算器计算：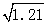
=，
=，
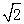≈；（保留三位小数）
（3）合并同类项：3a+2b+5a﹣8b=；
（4）如图，直线AB、CD相交于点O，OP平分∠BOD，若∠AOC=60°，则∠AOD=°，∠DOP=度．
（5）解方程：3x﹣7=x+1（写出过程）．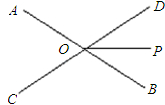
求一个正数的算术平方根，有些数可以直接求得，如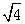
，有些数则不能直接求得，如
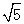，但可以通过计算器求得．还有一种方法可以通过一组数的内在联系，运用规律求得，请同学们观察下表：
| n |
16 |
0.16 |
0.0016 |
1600 |
160000 |
… |
 |
4 |
0.4 |
0.04 |
40 |
400 |
… |
（1）表中所给的信息中，你能发现什么规律？（请将规律用文字表达出来）
（2）运用你发现的规律，探究下列问题：
已知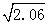
≈1.435，求下列各数的算术平方根：①0.0206；②206；③20600．
用四舍五入法按括号里的要求对下列各数取近似值．
（1）0.00149（精确到0.001）；
（2）204500（精确到千位）；
（3）0.08904（精确到千分位）．
把一个四位数x，先四舍五入到十位，得到的数为y，再四舍五入到百位，得到的数为z，再四舍五入到千位，恰好得到3000．
（1）原四位数x的最大值为多少？最小值为多少？
（2）将x的最大值与最小值的差用科学记数法表示出来（精确到千位）
小明和小刚测量同一根木棒，小明测得长是0.80m，小刚测得长是0.8m，问两人测量的结果是否相同？为什么？