如图甲所示,有一粒子源发射具有沿轴线ABO方向,速度大小不同的粒子,粒子质量均为m,带电荷量均为q(q>0)。A.B是两个阀门,阀门后是一对平行极板,两极板间距为2d,上极板接地,下极板的电势随时间变化关系如图乙所示。O处是一与轴线垂直的接收屏,以O为原点,垂直于轴线ABO向上为y坐标轴正方向。不同速度的粒子打在接收屏上对应不同的坐标,其余尺寸见图。已知关系式 。某时刻A开启,t/2后关闭,又经过t/2后B开启,再过t/2后B也关闭,以B开启的时刻作为图乙中计时零点。(不计粒子重力和粒子间的相互作用力)
。某时刻A开启,t/2后关闭,又经过t/2后B开启,再过t/2后B也关闭,以B开启的时刻作为图乙中计时零点。(不计粒子重力和粒子间的相互作用力)
(1)求能穿过A和B的粒子的最大速度和最小速度;
(2)上述两类粒子打在接收屏上的y坐标。
一位同学用单摆做测量重力加速度的实验,他将摆挂起后,进行了如下步骤
A.测摆长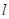 :用米尺量出摆线的长度.
:用米尺量出摆线的长度.
B.测周期 :将摆球拉起,然后放开,在摆球通过最低点时,按下秒表开始计时,同时将此次通过最低点作为第1次,接着一直数到摆球第60次通过最低点时,按秒表停止计时,读出这段时间
:将摆球拉起,然后放开,在摆球通过最低点时,按下秒表开始计时,同时将此次通过最低点作为第1次,接着一直数到摆球第60次通过最低点时,按秒表停止计时,读出这段时间 ,算出单摆的周期
,算出单摆的周期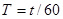 .
.
C.将所测得的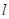 和
和 代入单摆的周期公式
代入单摆的周期公式 ,算出
,算出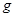 ,将它作为实验的最后结果写入报告中去.
,将它作为实验的最后结果写入报告中去.
指出上面步骤中遗漏或错误的地方,写出该步骤的字母,并加以改正,(不要求进行误差计算)________________________________________________________.
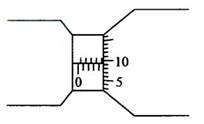
(1)某同学用螺旋测微器测量一铜丝的直径,测微器的示数如图所示,该铜丝的直径为
。
(2)右图为一电学实验的实物连线图。该实验可用来测量待测电阻
的阻值(约
). 图中两具电压表量程相同, 内阻都很大. 实验步骤如下: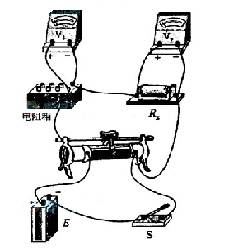
①调节电阻箱,使它的阻值R0与待测电阻的阻值接近;将滑动变阻器的滑动头调到最右端。
②合上开关
。
③将滑动变阻器的滑动头向左端滑动,使两个电压表指针都有明显偏转。
④记下两个电压表 和
和 的读数
和
。
的读数
和
。
⑤多次改变滑动变阻器滑动头的位置,记下 和
和 的多组读数
和
。
的多组读数
和
。
⑥求
的平均值。
回答下面问题:
(Ⅰ)根据实物连线图在虚线框内画出实验的电路原理图,其中电阻箱的符号为 ,滑动变阻器的符号为
,滑动变阻器的符号为 ,其余器材用通用的符号表示。
,其余器材用通用的符号表示。
(Ⅱ)不计电压表内阻的影响,用
、
和
表示
的公式为
=。
(Ⅲ)考虑电压表内阻的影响, 用
、
、
、 的内阻
、
的内阻
、 的内阻
表示
的公式为
=。
的内阻
表示
的公式为
=。
为了测定一个“6.3V、1W”的小电珠在额定电压下较准确的电阻值,可供选择的器材有:
A.电流表(0~3A,内阻约0.04Ω) B.毫安表(0~300mA,内阻约4Ω)
B.毫安表(0~300mA,内阻约4Ω)
C.电压表(0~10V,内阻10KΩ)
D.电压表(0~3V,内阻10KΩ)
E.电源(额定电压6V,最大允许电流2A)
F.电源(额定电压9V,最大允许电流1A)
G.可变电阻(阻值范围0~10Ω,额定电流1A)
H.可变电阻(阻值范围0~50Ω,额定功率0.5W)
I.导线若干根,电键一个.
(1)为使测量安全和尽可能准确,应选用的器材是.(用字母代号填写)
(2)请画出电路图,并把图7-3-10所示实物图用线连接起来.
一直流电压表,量程为1
,内阻为1
,现将一阻值为5000~
之间的固定电阻
与此电压表串联,以扩大电压表的量程。为求得扩大后量程的准确值,再给定一直流电源(电动势
为6~7
,内阻可忽略不计),一阻值
=
的固定电阻,两个单刀开关
及若干线.。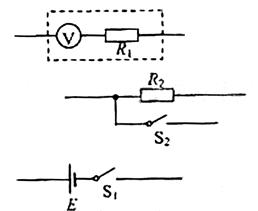
(1)为达到上述目的,将答题卡上对应的图连成一个完整的实验电路图。
(2)连线完成以后,当
与
均闭合时,电压表的示数为0.90
;当
闭合,
断开时,电压表的示数为0.70
,由此可以计算出改装后电压表的量程为V,电源电动势为
在做“用油膜法估测分子的大小”实验中,实验简要步骤如下:
| A.将画有油膜轮廓的玻璃板放在坐标纸上,数出轮廓内的方格数(不足半个的舍去,多于半个的算一个)再根据方格的边长求出油膜的面积S. |
| B.将一滴油酸酒精溶液滴在水面上,待油酸薄膜的形状稳定后,将玻璃板放在浅盘上,用彩笔将薄膜的形状描画在玻璃板上. |
| C.用浅盘装入约2 cm深的水,然后将痱子粉或石膏粉均匀地撒在水面. |
| D.用公式D=VS,求出薄膜厚度,即油酸分子的大小. |
E.根据油酸酒精溶液的浓度,算出一滴溶液中纯油酸的体积V.
F.用注射器或滴管将事先配制好的油酸酒精溶液一滴一滴地滴入量筒,记下量筒内增加一定体积时的滴数
上述实验步骤的合理顺序是____________________.