一粗细均匀的J型玻璃管竖直放置,左端封闭,右端(足够长)开口向上,左端封有一定质量的理想气体,初始状态左右两管水银面相平,如图所示.封闭气体的温度为27℃,大气压强为75cmHg.求: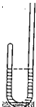
①若沿右侧管壁缓慢加入5cm长的水银柱并与下方的水银合为一体,为使封闭气体保持原来的长度,应使气体的温度变为多少?
②此过程封闭气体分子的平均动能(选填“增大”或“减小”),气体将 (选填“吸热”或“放热”)
如图所示,一长为l的长方形木块在水平面上以加速度a做匀加速直线运动。先后经过l、2两点,l、2之间有一定的距离,木块通过l、2两点所用时间分别为t1和t2。
求:(1)木块经过位置1、位置2的平均速度大小;
(2)木块前端P在l、2之间运动所需时间。
细绳一端系着质量M=8kg的物体静止在水平面,另一端通过光滑小孔吊着质量m=2kg的物体,M的中点与圆孔的距离r=0.2m,已知M与水平面间的动摩擦因数为0.2,现使此物体M随转台绕中心轴转动,问转台角速度ω在什么范围m会处于静止状态?(设最大静摩擦力等于滑动摩擦力,g="10" m/s2)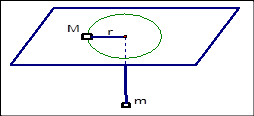
长L=0.5 m的轻杆,其一端连接着一个零件A,A的质量m=2 kg.现让A在竖直平面内绕O点做匀速圆周运动,如图所示.在A通过最高点时,求下列两种情况下杆对A的作用力的大小并指出是拉力还是支持力: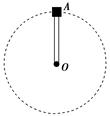
(1)A的速率为1 m/s;
(2)A的速率为4 m/s.(g=10 m/s2)
跳台滑雪是勇敢者的运动,它是利用依山势特别建造的跳台进行的。运动员穿着专用滑雪板,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆。这项运动极为壮观。设一位运动员由山坡顶的A点沿水平方向飞出,到山坡上的B点着陆。如图所示,已知运动员水平飞出的速度为v0= 20m/s,山坡倾角为θ= 37°,山坡可以看成一个斜面。(g = 10m/s2,sin37º= 0.6,cos37º= 0.8)求
(1)运动员在空中飞行的时间t
(2)AB间的距离s
长为L的细线,拴一质量为m的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图.求摆线L与竖直方向的夹角为α时:
(1)线的拉力F;
(2)小球运动的线速度的大小;
(3)小球运动的角速度及周期.