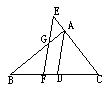
如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
一个正方体的骰子,1和6,2和5,3和4是分别相对的面上的点。现在有12个正方形格子的纸上画好了点状的图案,如图所示,若经过折叠能做成一个骰子,你认为应剪掉哪6个正方形格子?(请用笔在要剪掉的正方形格子上打“×”,不必写理由)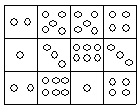
根据北京市统计局公布的2005年、2010年北京市人口数据,绘制统计图表如下:
2005年、2010年北京市常住人口中受教育程度情况统计表(人数单位:万人)
| 年份 |
大学程度人数(指大专及以上) |
高中程度人数(含中专) |
初中程度人数 |
小学程度人数 |
其他人数 |
| 2005年 |
233 |
320 |
475 |
234 |
120 |
| 2010年 |
362 |
372 |
476 |
212 |
114 |
请利用上述统计图表提供的信息回答下列问题:(1)从2005年到2010年北京市常住人口增加了多少万人?
(2)请结合2005年和2010年北京市常住人口受教育程度的状况,谈谈你的看法。
用正方体小木块搭建成的图形,下面三个图分别是它的主视图、俯视图、和左视图,请你观察它是由多少块小木块组成的
如图,CD平分∠ACB,DE∥AC,EF∥CD,求证:EF平分∠BED. 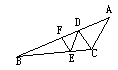
如图,AD平分∠BAC,点F在BD上,FE∥AD交AB于G,交CA的延长线于E,试说明:∠AGE=∠E.