一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,用列表或画树状的方法求两次摸出的球都是白球的概率.
如图,已知直线m∥n,A,B为直线n上的两点,C,D为直线m上的两点.
(1)请你判断△ABC与△ABD的面积具有怎样的关系;
(2)若点D在直线m上可以任意移动,△ABD的面积是否发生变化?并说明你的理由.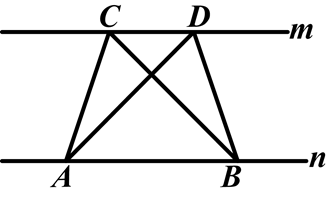
如图,已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
(1)如图(1),当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图(1),若CB=a,CE=2a,求BM,ME的长;
(3)如图(2),当∠BCE=45°时,求证:BM=ME.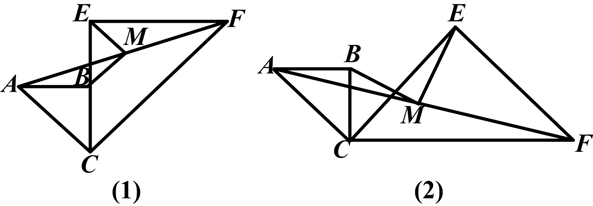
如图,已知A、B两地之间有一小池塘,小明为了测量A、B两地的距离,在AB一侧的开阔地取一点C,量取AC的中点D,BC的中点E,测量DE的长度,(1)小明这样做能得到A、B间的距离吗?(2)如果他量得DE=200m,那么A、B两地的距离为多少米?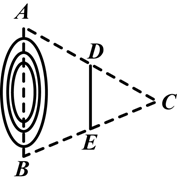
如图,在□ABCD中,F是AD的中点,延长BC到点E,使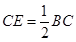 ,连接DE,CF.
,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
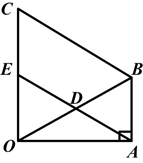
如图,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.求证:四边形ABCE是平行四边形.