我市某水产养殖中心,2014年鱼塘饲养鱼苗10千尾,平均每千尾鱼的产量为103千克,2015年计划继续向鱼塘投放鱼苗,每多投放鱼苗1千尾,每千尾的产量将减少50千克.
(1)今年应投放鱼苗多少千尾,可以使总产量达到10450千克?
(2)该水产养殖中心今年应投放鱼苗多少千尾,可以达到最大总产量?最大总产量是多少千克?
如图,直线AC∥BD,连结AB,直线AB、BD、AC把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线组成的角是0度角.)
(1)当动点P落在第①部分时,试说明∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③、④部分时,全面探究∠APB、∠PAC、∠PBD之间的数量关系,并画出相应的图形、写出相应的结论.请选择一种结论加以说明.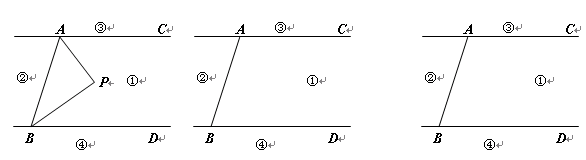
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.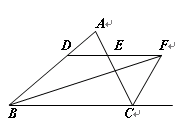
(1)试说明BD=DF;
(2)请写出图中所有的等腰三角形;
(3)线段BD,CE,DE之间存在怎样的数量关系?请说明理由.
如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F.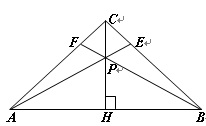
(1)试说明∠CAE=∠CBF;
(2)AE和BF 是否相等?请说明理由.
如图,已知AB∥CD,∠1=40º,∠2=70º,求出∠3,∠4的度数.
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点.
(1)试说明BE=CD;
(2)请用一句话叙述由第(1)小题得出的结论.