如图，把△OAB放置于平面直角坐标系xOy中，∠OAB=90°，OA=2，AB=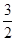
，把△OAB沿x轴的负方向平移2OA的长度后得到△DCE．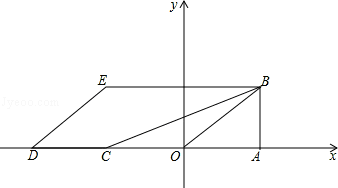
（1）若过原点的抛物线y=ax2+bx+c经过点B、E，求此抛物线的解析式；
（2）若点P在该抛物线上移动，当点p在第一象限内时，过点p作PQ⊥x轴于点Q，连接OP．若以O、P、Q为定点的三角形与以B、C、E为定点的三角形相似，直接写出点P的坐标；
（3）若点M（﹣4，n）在该抛物线上，平移抛物线，记平移后点M的对应点为M′，点B的对应点为B′．当抛物线向左或向右平移时，是否存在某个位置，使四边形M′B′CD的周长最短？若存在，求出此时抛物线的解析式；若不存在，请说明理由．
解下列不等式，并将解集分别用数轴表示出来：
（1）
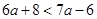（2）
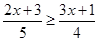
丰富的图形世界里有奇妙的数量关系，让我们通过下面这些几何体开始神奇的探索之旅．
观察：下面这些几何体都是简单几何体，请您仔细观察．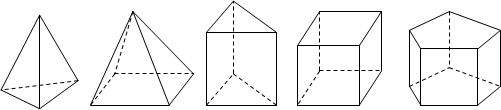
统计：每个几何体都会有棱（棱数为E）、面（面数为F）、顶点（顶点数为V），现将有关数据统计，完成下表．
| 几何体 |
a |
b |
c |
d |
e |
| 棱数（E） |
6 |
9 |
15 |
||
| 面数（F） |
4 |
5 |
5 |
6 |
|
| 顶点数（V） |
4 |
5 |
8 |
发现：（1）简单几何中，
；
（2）简单几何中，每条棱都是个面的公共边；
（3）在正方体中，每个顶点处有条棱，每条棱都有个顶点，所以有2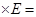
3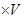
．
应用：有一个叫“正十二面体”的简单几何体，它有十二个面，每个面都是正五边形，它的每个顶点处都有相同数目的棱．请问它有条棱，个顶点，每个顶点处有条棱．
问题：山中有古寺，不知道住着多少僧人，只知道用餐时，他们三个人合用一只碗吃饭，四个人合用一只碗喝汤，不多不少共用了224只碗．这个寺内一共有多少名僧人？
为了解决这个问题，同学们分别想了许多办法．同学甲直接设寺内有僧人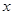
名，同学乙则设用去饭碗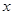只．你知道这两名同学分别是如何解决问题的吗？请你分别写出他们的解题过程．
如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°．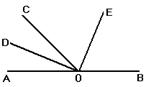
（1）请你数一数，图中有多少个小于平角的角；
（2）求出∠BOD的度数；
（3）试判断OE是否平分∠BOC，并说明理由．
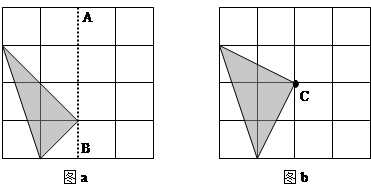
（1）在图a空白的方格中，画出阴影部分的图形沿虚线AB翻折后的图形；
（2）在图b空白的方格中，画出阴影部分的图形绕点C旋转180°后的图形．