某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），
（1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．
正方形ABCD的边长为3，E，F 分别是AB，BC边上的点，且∠EDF=45°．将
△DAE绕点D逆时针旋转90°，得到△DCM．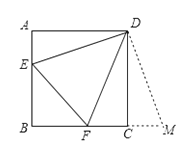
（1）求证：EF=FM；
（2）当AE=1时，求EF的长．
如图，在△ABC中，∠B=90°，AB="6" cm，BC="8" cm．将△ABC沿射线BC方向平移10 cm，得到△DEF，A，B，C的对应点分别是D，E，F，连接AD．求证：四边形ACFD是菱形．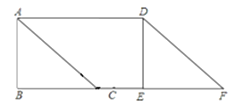
用反证法证明：在一个三角形中，如果两条边不相等，那么这两条边所对的角也不相等.
如图，在四边形ABCD中，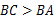
，
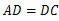，BD平分∠ABC.
求证：∠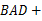
∠
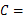180°.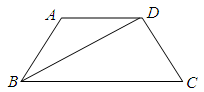
如图，在△ABC中，∠B=90°，M是AC上任意一点（M与A不重合），MD⊥BC，MD交∠BAC的平分线于点D，求证：
.