阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解∵x﹣y=2,∴x=y+2.
又∵x>1,∴y+2>1.
∴y>﹣1.
又∵y<0,∴﹣1<y<0.…①
同理得:1<x<2. …②
由①+②得﹣1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
(1)已知x﹣y=4,且x>3,y<1,则x+y的取值范围是 .
(2)已知y>1,x<﹣1,若x﹣y=m成立,求x+y的取值范围(结果用含m的式子表示).
解方程 (本题6分)
(1)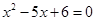
(2)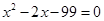
(本题6分)先化简,再求值: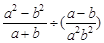 ,其中
,其中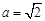 ,
,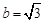 .
.
如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.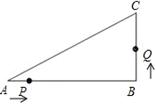
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
已知:如图,D是△ABC的BC边上的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF.求证: △ABC是等腰三角形.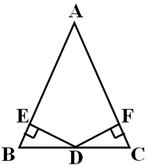
如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且∠ABC=90°,连接AC.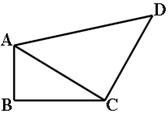
(1)求AC的长度;
(2)试判断三角形ACD的形状.