如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（﹣12，16），矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．
（1）直接写出线段BO的长；
（2）求直线BD解析式；
（3）若点N在直线BD上，在x轴上是否存在点M，使以M、N、E、D为顶点的四边形是平行四边形？若存在，请求出一个满足条件的点M的坐标；若不存在，请说明理由．
(本题满分8分) (1)解方程：3x2+7x+2=0．
(2)解不等式组
(本题满分8分)计算：(1)（-3）0-+|1-|
（2）先化简，再求值：(4ab3－8a2b2)÷4ab＋(2a＋b)(2a－b)，其中a＝2，b＝1．
（本小题满分7分）如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，2OB=OD，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合)，
PQ∥y轴与抛物线交于点Q.
 |
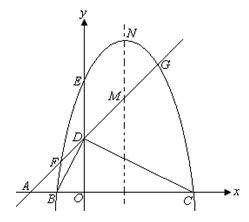(1)求经过B、E、C三点的抛物线的解析式；
(2)是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由；
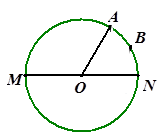
（本小题满分7分）如图，点A是半圆上的一个三等分点，点B是弧AN的中点，点P是直径MN上一个动点，圆O的半径为1，（1）找出当AP＋BP能得到最小值时，点P的位置，并证明
（2）求出AP＋BP最小值
（本小题满分6分）在直角坐标平面中，O为坐标原点，二次函数
的图象与x轴的负半轴相交于点C（如图），点C的坐标为（0，－3），且BO＝CO(1)求这个二次函数的解析式；
(2)设这个二次函数的图象的顶点为M，求AM的长.
