(本题6分)探索与思考:
观察下列等式: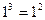
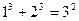
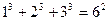
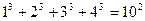
……………………(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?
(2)试一试:13 + 23 + 3 3 + 43 + … + 10 3= ____________.
(3)猜一猜:可得出什么规律(可用带字母的等式表示,也可用文字表述):
(本题6分)已知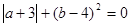 ,试求
,试求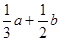 的值。
的值。
(4分)在数轴上表示下列各数,并用“<”连接起来。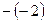 ,
,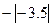 ,
,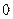 ,
,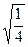 ,
,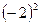 ,
,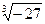 。
。
某军加油飞机接到命令,立即给另一架正在飞行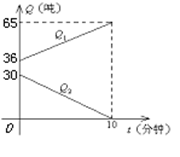
的运输飞机进行空中加油.在加油的过程中,
设运输飞机的油箱余油量为Q1吨,加油飞机的
加油油箱的余油量为Q2吨,加油时间为t分钟,
Q1、Q2与t之间的函数关系如图.回答问题:(1) 加油飞机的加油油箱中装载了多少吨油?
将这些油全部加给运输飞机需要多少分钟?(2) 求加油过程中,运输飞机的余油量Q1(吨)
与时间t(分钟)的函数关系式;(3) 运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?
请通过计算说明理由.
已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7. 2厘米,求这个一次函数的关系式.