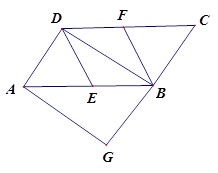
如图,在□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG//DB交CB的延长线于点G.求证:DE∥BF;
若∠G=90°,求证四边形DEBF是菱形.
中山市体育中考现场考试内容有三项:50米跑为必测项目;另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项每位考生有__________种选择方案;
用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种主案用
 、…或①、②、③、…等符号来代表可简化解答过程)
、…或①、②、③、…等符号来代表可简化解答过程)
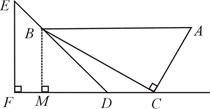
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长。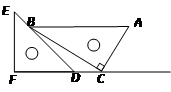
小明乘坐火车从某地到上海去参观世博园,已知此次行程为2160千米,城际直达动车组的平均时速是特快列车的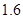 倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.
倍.小明购买火车票时发现,乘坐动车组比乘坐特快列车少用6小时.求小明乘坐动车组到上海需要的时间.
已知关于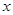 的一元二次方程
的一元二次方程 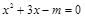 有实数根.
有实数根.求
 的取值范围
的取值范围若两实数根分别为
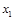 和
和 ,且
,且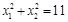 求
求 的值.
的值.