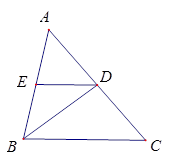
探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
某中学为创建绿色和谐校园,拟在一块三角形花圃里从点A修建一条花间小路到边BC. (不要求尺规作图)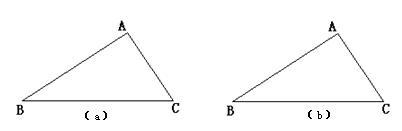
若要使修建的小路路程最短,请在图(a)中画出小路AD.
所根据的数学原理是__________________________________;若要在小路两边种植两种不同的花草,且使它们的种植面积相等,请在图(b)中画出小路AE.
如图,把 的
的 点平移到
点平移到 ,
,
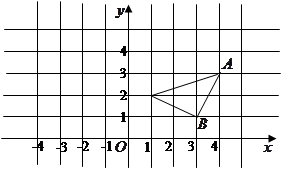
画出
写出另外两个点
 ,
,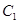 的坐标
的坐标
如图所示,直线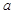 ∥
∥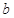 .直线
.直线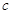 与直线
与直线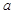 ,
,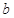 分别相交于点
分别相交于点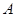 、点
、点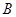 ,
,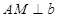 ,垂足为点
,垂足为点 ,若
,若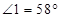 ,求
,求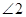 的度数.
的度数.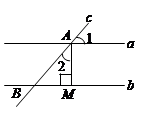
已知:如图,在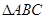 中,
中,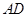 是
是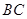 边上的高,
边上的高,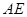 是
是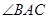 平分线.
平分线.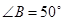 ,
,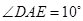 。
。求
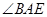 的度数;
的度数;求
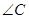 的度数.
的度数.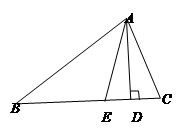
如图,△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,∠A=60°,∠BDC=100°求∠BDE的度数。