AB∥CD，点C在点D的右侧，∠ABC，∠ADC的平分线交于点E（不与B，D点重合）．∠ABC=n°，∠ADC=80°．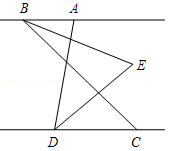
（1）若点B在点A的左侧，求∠BED的度数（用含n的代数式表示）；
（2）将（1）中的线段BC沿DC方向平移，当点B移动到点A右侧时，请画出图形并判断∠BED的度数是否改变．若改变，请求出∠BED的度数（用含n的代数式表示）；若不变，请说明理由．
在△ABC中，∠C=30°，AC=4cm,AB=3cm，求BC的长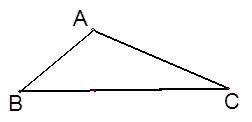
一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分到达目的地.求前一小时的行驶速度.
如图，在5×5的正方形网格中，每个小正方形的边长都为1，请在所给网格中解答下面问题。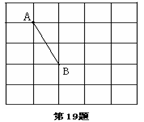
图中线段AB的两端点都落在格点（即小正方形的顶点）上，求出AB的长度
再以AB为一边画一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数；
请直接写出符合(2)中条件的等腰三角形ABC的顶点C的个数.
如图，一次函数
的图像与反比例函数
的图像交于
两点。
的值；求一次函数的解析式；
若直线AB交
轴于点C，求△OBC的面积根据图象写出使一次函数的值小于反比例函数的值的x的取值范围
阅读下列解题过程：已知a，b，c为△ABC的三边，且满足a2c2－b2c2＝a4－b4，试判断△ABC的形状。
解：∵ a2c2－b2c2＝a4－b4，①
∴ c2（a2－b2）＝（a2 + b2）（a2－b2），②
∴ c2＝ a2+b2，③
∴ △ABC为直角三角形。
问：上述解题过程，从哪一步开始出现错误？请写出该步的代号；
该步正确的写法应是
本题正确的结论应是