如图,正方形ABCD中,点E在对角线AC上,连接EB.ED.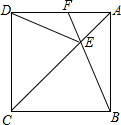
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140°,求∠AFE的度数.
(本小题满分7分)完成下列各题:
(1)计算:  ;
;
(2)先化简,再求值: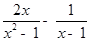 ,其中
,其中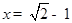 .
.
设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.
(1)求抛物线的解析式和顶点M的坐标;
(2)当∠APB=90°时,求P点坐标;
(3)连接AC,过P点做直线PE∥AC交x轴于点E,是否存在一点P,使以点A、C、P、E为顶点的四边形为平行四边形.若不存在试说明理由;若存在,试求出点P的坐标.
(本小题满分10分)如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF,BD⊥CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时, AC与BG的交点为M, 当AB=4,AD= 时,求线段CM的长.
时,求线段CM的长.
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)当BC=4,AC=3CE时,求⊙O的半径.
某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
| 类型价格 |
进价(元/盏) |
售价(元/盏) |
| A型 |
30 |
45 |
| B型 |
50 |
70 |
(1)若商场预计进货款为3500元,则这两种台灯各购进多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?