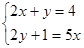老王是新农村建设中涌现出的“养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产出情况如表:
| |
鱼苗投资 (百元) |
饲料支出 (百元) |
收获成品鱼 (千克) |
成品鱼价格 (百元/千克) |
| A种鱼 |
2 |
3 |
100 |
0.1 |
| B种鱼 |
4 |
5 |
55 |
0.4 |
(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)
(1)按目前市场行情,老王养殖A、B两种淡水鱼获得利润最多是多少万元?
(2)基础建设投入、鱼苗投资、饲料支出及产量不变,但当老王的鱼上市时,A种鱼价格上涨a%,B种鱼价格下降20%,使老王养鱼实际获得利润5.68万元.求a的值.
甲、乙两个车间工人人数不相等,若甲车间调10人到乙车间,则两车间人数相等;若乙车间调10人到甲车间,则甲车间的人数就是乙车间人数的2倍,求原来甲、乙两车间各有多少名工人?
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表: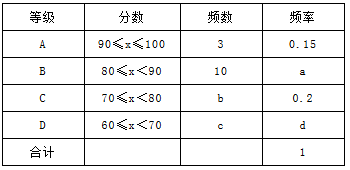
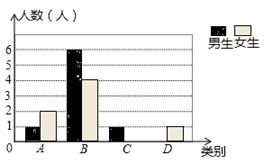
请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
如图所示,在所给的平面直角坐标系中,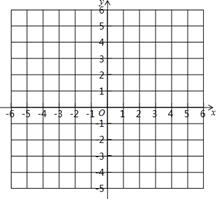
(1)描出下列各点,并将A、B、C三点顺次连接起来
A(2,3)、B(—2,—1)、C(3,2)
(2)将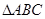 向左平移2个单位长度,向下平移1个单位长度,得到
向左平移2个单位长度,向下平移1个单位长度,得到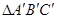 ,则点
,则点 的对应点
的对应点 的坐标为 ;点
的坐标为 ;点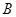 的对应点
的对应点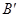 的坐标为 ;点
的坐标为 ;点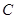 的对应点
的对应点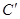 的坐标为
的坐标为
解下列不等式组,并把解集表示在数轴上
(1)
(2)
解方程组