夏季来临，商场准备购进甲、乙两种空调．已知甲种空调每台进价比乙种空调多500元，用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同．请解答下列问题：
（1）求甲、乙两种空调每台的进价；
（2）若甲种空调每台售价2500元，乙种空调每台售价1800元，商场欲同时购进两种空调20台，且全部售出，请写出所获利润y（元）与甲种空调x（台）之间的函数关系式；
（3）在（2）的条件下，若商场计划用不超过36000元购进空调，且甲种空调至少购进10台，并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器．直接写出购买按摩器的方案．
已知，如图1，抛物线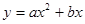
过点
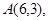且对称轴为直线
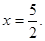点Ｂ为直线OA下方的抛物线上一动点，点B的横坐标为m.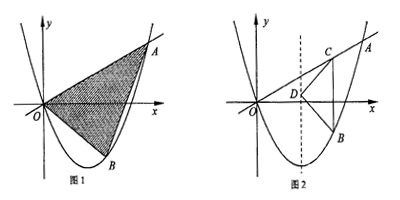
（1）求该抛物线的解析式：
（2）若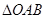
的面积为S．求S关于m的函数关系式，并求出S的最大值．
（3）如图2，过点B作直线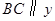
轴，交线段OA于点C，在抛物线的对称轴上是否存在点D，使
是以D为直角顶点的等腰直角三角形？若存在，求出所有符合条件的点B的坐标，若不存在，请说明理由．
如图，已知AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC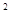
=PE·PO .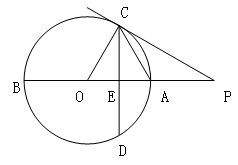
（1）求证：PC是⊙O的切线；
（2）若OE:EA=1：2，PA=6，求⊙O的半径；
（3）在（2）问下，求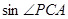
的值。
某中学库存960套旧课桌椅准备修理。现有甲、乙两个木工小组都想承接这项业务。经协商后得知：甲小组单独修理这批桌椅比乙小组多用20天；乙小组每天比甲小组多修8套；学校每天需付甲小组修理费80元，付乙小组120元。
（1）求甲、乙两个小组每天各修理桌櫈多少套？
（2）在修理过程中，学校要委派一名修理工进行质量监督，并由学校负担他每天的生活补助10元，现有以下三种修理方案供选择：①由甲单独修理；②由乙单独修理；③由甲、乙共同合作修理。你认为哪种方案既省时又省钱？试比较说明。
如图，在等腰梯形ABCD中，AD∥BC，AD=3cm，BC=7cm，∠B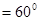
,P为下底BC边上一点（不与B、C重合），连结AP，过P点作PE交DC于E，使得∠APE=∠B.
(1)求证：△ABP∽△PCE；
(2)求腰AB的长；
(3)在底边BC上是否存在一点P，使得DE:EC=5:3.如果存在，求出BP的长；如果不存在，请说明理由。
如图，一次函数的图象与反比例函数的图象相交于A、B两点。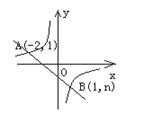
（1）利用图中的条件，求反比例函数和一次函数的表达式；
（2）根据图象写出使一次函数的值大于反比例函数的值的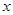
的取值范围；
（3）求△ABO的面积。